PK02 - One-compartment oral dosing

1 Learning Outcome

By the application of the present model, we will learn how to model orally-administered drug data with a first order input model with and without a lag-time.

2 Objectives

In this exercise, you will learn how to:

  • Simulate an Oral One Compartment (with/without lag-time) model (assuming oral bioavailability of 100%). Remember, since this is an oral medication, the interpretation of V includes bioavailability (i.e., it is really estimating V/F).
  • Write a differential equation for a one-compartment model.

3 Background

Before constructing a model, it is important to establish the process the model will be following and a scenario for the simulation.

Below is the scenario for this tutorial:

  • Structural model - 1 compartment with first order absorption (without/with Lag time)
  • Route of administration - Oral
  • Dosage Regimen - 100 μg Oral
  • Number of Subjects - 1

This diagram describes how such an administered dose will be handled, which facilitates building the model. 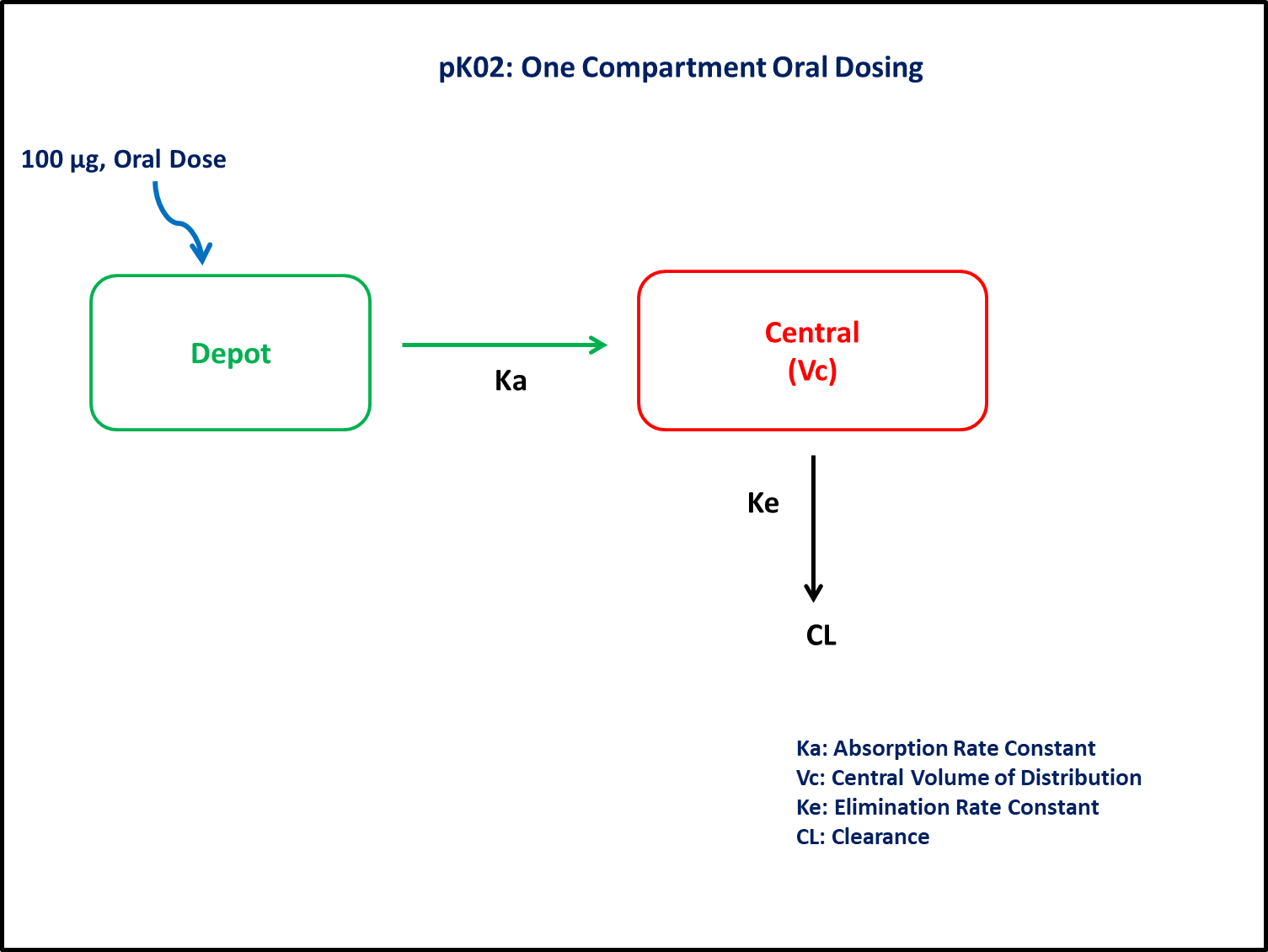PK02 Dosing Graphic Model

4 Libraries

Call the required libraries to get started.

using Pumas
using PumasUtilities
using Random
using CairoMakie
using AlgebraOfGraphics
using DataFramesMeta
using CSV

5 Model

In this one compartment model, we administer the dose in Depot compartment at time = 0.

Addition to Model Blocks

Take note that this model includes a lag time in the @param and @dosecontrol blocks.

pk_02 = @model begin
    @metadata begin
        desc = "One Compartment Model with lag time"
        timeu = u"minute"
    end

    @param begin
        """
        Absorption rate constant (1/min)
        """
        tvka ∈ RealDomain(; lower = 0)
        """
        Elimination rate constant (1/min)
        """
        tvkel ∈ RealDomain(; lower = 0)
        """
        Volume (L)
        """
        tvvc ∈ RealDomain(; lower = 0)
        """
        Lag Time (mins)
        """
        tvlag ∈ RealDomain(; lower = 0)
        Ω ∈ PDiagDomain(3)
        """
        Proportional RUV
        """
        σ²_prop ∈ RealDomain(; lower = 0)
    end

    @random begin
        η ~ MvNormal(Ω)
    end

    @pre begin
        Ka = tvka * exp(η[1])
        Kel = tvkel * exp(η[2])
        Vc = tvvc * exp(η[3])
    end

    @dosecontrol begin
        lags = (Depot = tvlag,)
    end

    @dynamics begin
        Depot' = -Ka * Depot
        Central' = Ka * Depot - Kel * Central
    end

    @derived begin
        """
        Concentration (μg/L)
        """
        cp = @. Central / Vc
        """
        Concentration (μg/L)
        """
        dv ~ @. Normal(cp, sqrt(cp^2 * σ²_prop))
    end
end
PumasModel
  Parameters: tvka, tvkel, tvvc, tvlag, Ω, σ²_prop
  Random effects: η
  Covariates:
  Dynamical system variables: Depot, Central
  Dynamical system type: Matrix exponential
  Derived: cp, dv
  Observed: cp, dv
Take note of the derived block!
  1. Do not forget the @..
  2. Be sure to code for the correct Residual Unexplained Variability (RUV) in the derived block. This is an example of a model with proportional RUV.

6 Parameters

The compound follows a one compartment model, in which the various parameters are as mentioned below:

  • Ka - Absorption Rate Constant (min⁻¹)
  • Kel - Elimination Rate Constant (min⁻¹)
  • Vc - Central Volume of distribution (L)
  • tlag - Lag-time (min)
  • Ω - Between Subject Variability
  • σ - Residual error

These are the initial estimates we will be using in this model exercise. tv represents the typical value for parameters.

The first set of estimates does not include lag time and has the typical values for absorption rate constant tvka and elimination rate constant tvkel as the same values.

The second set of estimates includes a lag time estimate and has different values for tvka and tvkel.

param = [
    (
        tvka = 0.013,
        tvkel = 0.013,
        tvvc = 32,
        tvlag = 0,
        Ω = Diagonal([0.01, 0.01, 0.01]),
        σ²_prop = 0.015,
    ),
    (
        tvka = 0.043,
        tvkel = 0.0088,
        tvvc = 32,
        tvlag = 16,
        Ω = Diagonal([0.01, 0.01, 0.01]),
        σ²_prop = 0.015,
    ),
]

7 Dosage Regimen

To start the simulation process, the dosing regimen from the background section must be developed first prior to running a simulation.

In this section, the DosageRegimen is mentioned:

  • Oral dosing of 100 μg at time=0

This is how to establish the dosing regimen:

ev1 = DosageRegimen(100; time = 0, cmt = 1)
1×10 DataFrame
Row time cmt amt evid ii addl rate duration ss route
Float64 Int64 Float64 Int8 Float64 Int64 Float64 Float64 Int8 NCA.Route
1 0.0 1 100.0 1 0.0 0 0.0 0.0 0 NullRoute

This is how to create a population of 2 subjects receiving the dosing regimen above. The first subject is simulated with the “No lag”, parameters and the second subject is simulated with the “With Lag” parameters, as they were specified above.

pop = map(i -> Subject(id = i, events = ev1), ["1: No Lag", "2: With Lag"])
Population
  Subjects: 2
  Observations:

8 Simulation

Note

The Random.seed! function is included here for purposes of reproducibility of the simulation in this tutorial. Specification of a seed value would not be required in a Pumas workflow that is estimating model parameters.

Random.seed!(123)

Perform the simulation step.

sim = map(zip(pop, param)) do (subj, p)
    return simobs(pk_02, subj, p, obstimes = 0:1:400)
end
Simulated population (Vector{<:Subject})
  Simulated subjects: 2
  Simulated variables: cp, dv

9 Visualize results

From the plot below, we can clearly identify the subject with and without lag time.

@chain DataFrame(sim) begin
    dropmissing(:cp)
    data(_) *
    mapping(:time => "Time (minutes)", :cp => "Concentration (μg/L)"; color = :id => "") *
    visual(Lines; linewidth = 4)
    draw(; figure = (; fontsize = 22))
end

10 Population Simulation

This block updates the parameters of the model to increase intersubject variability in parameters and defines the time points for the predicted concentrations. The results are written to a CSV file.

par = (
    tvka = 0.043,
    tvkel = 0.0088,
    tvvc = 32,
    tvlag = 16,
    Ω = Diagonal([0.04, 0.09, 0.015]),
    σ²_prop = 0.03,
)

ev1 = DosageRegimen(100; time = 0, cmt = 1)
pop = map(i -> Subject(; id = i, events = ev1), 1:100)

Random.seed!(1234)
pop_sim = simobs(
    pk_02,
    pop,
    par,
    obstimes = [0, 10, 15, 20, 30, 40, 60, 90, 120, 180, 210, 240, 300, 360],
)
df_sim = DataFrame(pop_sim)
CSV.write("pk_02.csv", df_sim)
"pk_02.csv"
Saving the Simulation Results

With the CSV.write function, you can input the name of the dataframe (df_sim) and the file name of your choice (pk_02.csv) to save the file to your local directory or repository.

11 Conclusion

This tutorial has demonstrated constructing a one compartment model in Pumas.

We describe the:

  • model structure for the process of the drug passing through the system,
  • translating processes into ODEs using Pumas, and
  • simulating the model in a single patient, with and without an absorption lagtime.