PK05 - One-compartment intravenous plasma/urine I

1 Learning Outcome

In this model, both plasma and urine data are collected, which will help to estimate parameters like Clearance, Volume of Distribution and fraction of dose excreted unchanged in urine.

2 Objectives

In this tutorial, you will learn how to:

  • Build a one compartment model of a medication that undergoes excretion via urine
  • Simulate the model for a single subject and a single dosing regimen, and
  • Fit the model to data containing urine sample information

3 Background

Before constructing a model, it is important to establish the process the model will follow and a scenario for the simulation.

Below is the scenario for this tutorial:

  • Structural Model - One Compartment Model with urinary excretion
  • Route of Administration - Intravenous Bolus
  • Dosage Regimen - 250 mg IV Bolus
  • Subject - 1

This diagram describes how such an administered dose will be handled, which facilitates building the model. 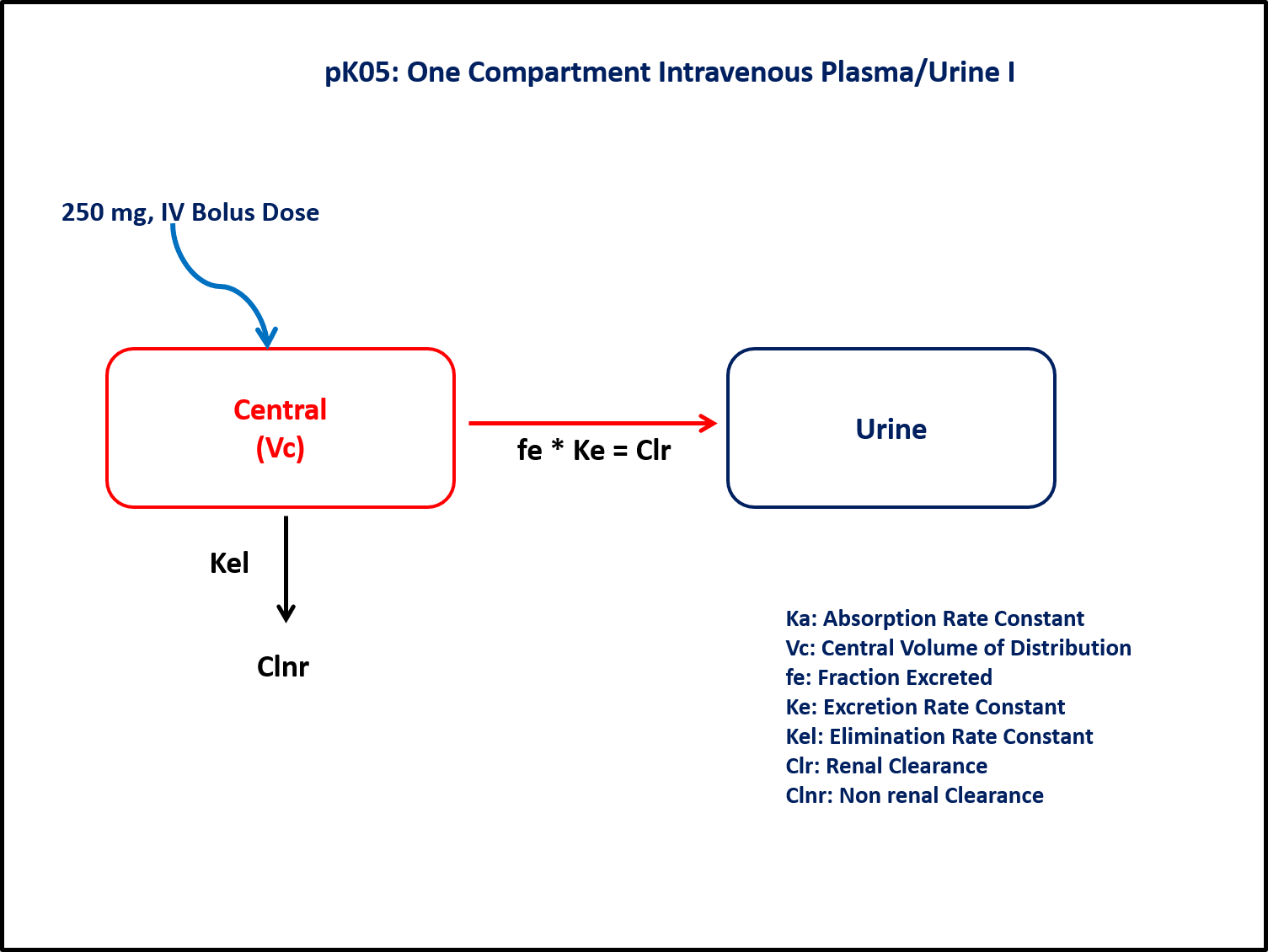PK05 Graphic Model

4 Libraries

Call the required libraries to get started.

using Pumas
using PumasUtilities
using Random
using CairoMakie
using AlgebraOfGraphics
using DataFramesMeta

5 Model

In this one compartment model, we administer an IV dose in the central compartment.

New Urine Compartment in @dynamics

In the @dynamics block, a Urine Compartment is included. This measures the rate of change in amount over time and calculates the cumulative amount of drug in urine.

pk_05 = @model begin
    @metadata begin
        desc = "One Compartment Model with Urine Compartment"
        timeu = u"hr"
    end

    @param begin
        """
        Volume of Distribution (L)
        """
        tvvc ∈ RealDomain(lower = 0)
        """
        Renal Clearance(L/hr)
        """
        tvClr ∈ RealDomain(lower = 0)
        """
        Non Renal Clearance(L/hr)
        """
        tvClnr ∈ RealDomain(lower = 0)
        Ω ∈ PDiagDomain(3)
        """
        Proportional RUV - Plasma
        """
        σ_prop ∈ RealDomain(lower = 0)
        """
        Additive RUV - Urine
        """
        σ_add ∈ RealDomain(lower = 0)
    end

    @random begin
        η ~ MvNormal(Ω)
    end

    @pre begin
        Clr = tvClr * exp(η[1])
        Clnr = tvClnr * exp(η[2])
        Vc = tvvc * exp(η[3])
    end

    @dynamics begin
        Central' = -(Clnr / Vc) * Central - (Clr / Vc) * Central
        Urine' = (Clr / Vc) * Central
    end

    @derived begin
        """
        PK05 Plasma Concentration (mg/L)"
        """
        cp_plasma = @. Central / Vc
        dv_plasma ~ @. Normal(cp_plasma, abs(cp_plasma) * σ_prop)

        """
        PK05 Urine Amount (mg)
        """
        cp_urine = @. Urine
        dv_urine ~ @. Normal(cp_urine, abs(σ_add))
    end
end
PumasModel
  Parameters: tvvc, tvClr, tvClnr, Ω, σ_prop, σ_add
  Random effects: η
  Covariates:
  Dynamical system variables: Central, Urine
  Dynamical system type: Matrix exponential
  Derived: cp_plasma, dv_plasma, cp_urine, dv_urine
  Observed: cp_plasma, dv_plasma, cp_urine, dv_urine

6 Parameters

The parameters to define and estimate using the model are as mentioned below:

  • Clnr - Non renal Clearance (L/hr)
  • Clr - Renal Clearance (L/hr)
  • Vc - Volume of the Central Compartment(L)
  • Ω - Between subject variability
  • σ - Residual Error

These are the initial estimates we will be using in this model exercise. Note that tv represents the typical value for parameters.

param = (;
    tvvc = 10.7965,
    tvClr = 0.430905,
    tvClnr = 0.779591,
    Ω = Diagonal([0.01, 0.01, 0.01]),
    σ_prop = 0.1,
    σ_add = 1,
)

7 Dosage Regimen

To start the simulation process, the dosing regimen from the background section must be developed first. From our background, we established the scenario as a single dose of 250 mg given as an Intravenous bolus to a single subject.

The DosageRegimen is specified as:

ev1 = DosageRegimen(250; time = 0, cmt = 1)
1×10 DataFrame
Row time cmt amt evid ii addl rate duration ss route
Float64 Int64 Float64 Int8 Float64 Int64 Float64 Float64 Int8 NCA.Route
1 0.0 1 250.0 1 0.0 0 0.0 0.0 0 NullRoute

This is how to create the single subject undergoing the dosing regimen above.

sub = Subject(; id = 1, events = ev1)
Subject
  ID: 1
  Events: 1

8 Simulation

Let’s simulate the plasma concentration and the unchanged amount excreted in urine.

Random.seed!()

The Random.seed! function is included here for purposes of reproducibility of the simulation in this tutorial. Specification of a seed value would not be required in a Pumas workflow that is estimating model parameters.

Random.seed!(123)
sim_sub1 = simobs(pk_05, sub, param, obstimes = 0:0.1:26)
SimulatedObservations
  Simulated variables: cp_plasma, dv_plasma, cp_urine, dv_urine
  Time: 0.0:0.1:26.0

9 Visualization

These figures display the drug concentration levels in both plasma and urine samples.

variable_renamer = renamer(
    "cp_plasma" => "Plasma \n concentration (mg/L)",
    "cp_urine" => "Urine \n amount (mg)",
)

plot_df = @chain DataFrame(sim_sub1) begin
    @select :id :time :cp_plasma :cp_urine
    dropmissing([:cp_plasma, :cp_urine])
    stack(Not(:id, :time))
end

plt_rows =
    data(plot_df) *
    mapping(:time => "Time (hours)", :value => "", row = :variable => variable_renamer) *
    visual(Lines; linewidth = 4)

draw(plt_rows; figure = (; fontsize = 22), facet = (; linkyaxes = :none))

By looking at the figure, we can observe that the drug level is decreasing in plasma and increasing in the urine, which resembles normal physiologic function.

When we put the visualization together, we observe the following figure:

plt_join =
    data(plot_df) *
    mapping(
        :time => "Time (hours)",
        :value => "Concentration / Amount",
        color = :variable => variable_renamer => "",
    ) *
    visual(Lines; linewidth = 4)

draw(plt_join; figure = (; fontsize = 22), legend = (; position = :bottom))

10 Population Simulation

This block updates the parameters of the model to increase intersubject variability in parameters and defines timepoints for prediction of concentrations. The results are written to a CSV file.

par = (
    tvvc = 10.7965,
    tvClr = 0.430905,
    tvClnr = 0.779591,
    Ω = Diagonal([0.04, 0.09, 0.0225]),
    σ_prop = 0.0256,
    σ_add = 3.126,
)

ev1 = DosageRegimen(250; time = 0, cmt = 1)
pop = map(i -> Subject(id = i, events = ev1), 1:55)

Random.seed!(1234)
pop_sim = simobs(pk_05, pop, par, obstimes = [0.5, 1, 1.5, 2, 4, 6, 8, 12, 18, 24])
sim_plot(pop_sim)

df_sim = DataFrame(pop_sim)

#CSV.write("pk_05.csv", df_sim)
Saving the Simulation Results

With the CSV.write function, you can input the name of the dataframe (df_sim) and the file name of your choice (pk_05.csv) to save the file to your local directory or repository.

11 Conclusion

Constructing a one compartment model with urine elimination involves:

  • understanding the process of how the drug is passed through the system,
  • translating processes into ODEs using Pumas,
  • explaining the drug elimination process in Pumas, and
  • simulating the model in a single patient for evaluation.