using Pumas
using PumasUtilities
using Random
using CairoMakie
using AlgebraOfGraphics
using CSV
using DataFramesMeta
PK32 - Turnover III - Non-linear Disposition
1 Learning Outcomes
In this tutorial, we will learn to simulate data for multiple infusions of an endogenous compound with non-linear disposition.
2 Objectives
In this exercise, you will learn how to:
- Build a one compartment model for an endogenous compound with non-linear disposition
- Use final parameter estimates and design a multiple infusion dosage regimen
- Simulate and plot a single subject with predefined time points.
3 Background
Before constructing a model, it is important to establish the process the model will follow and a scenario for the simulation.
Below is the scenario for this tutorial:
- Structural model - One compartment with zero order input and non linear elimination
- Route of administration - IV infusion
- Dosage Regimen - Multiple intravenous infusions (three sets of rapid IV infusions followed by a slow IV infusion)
- Number of Subjects - 1
This diagram describes how such an administered dose will be handled, which facilitates building the model. 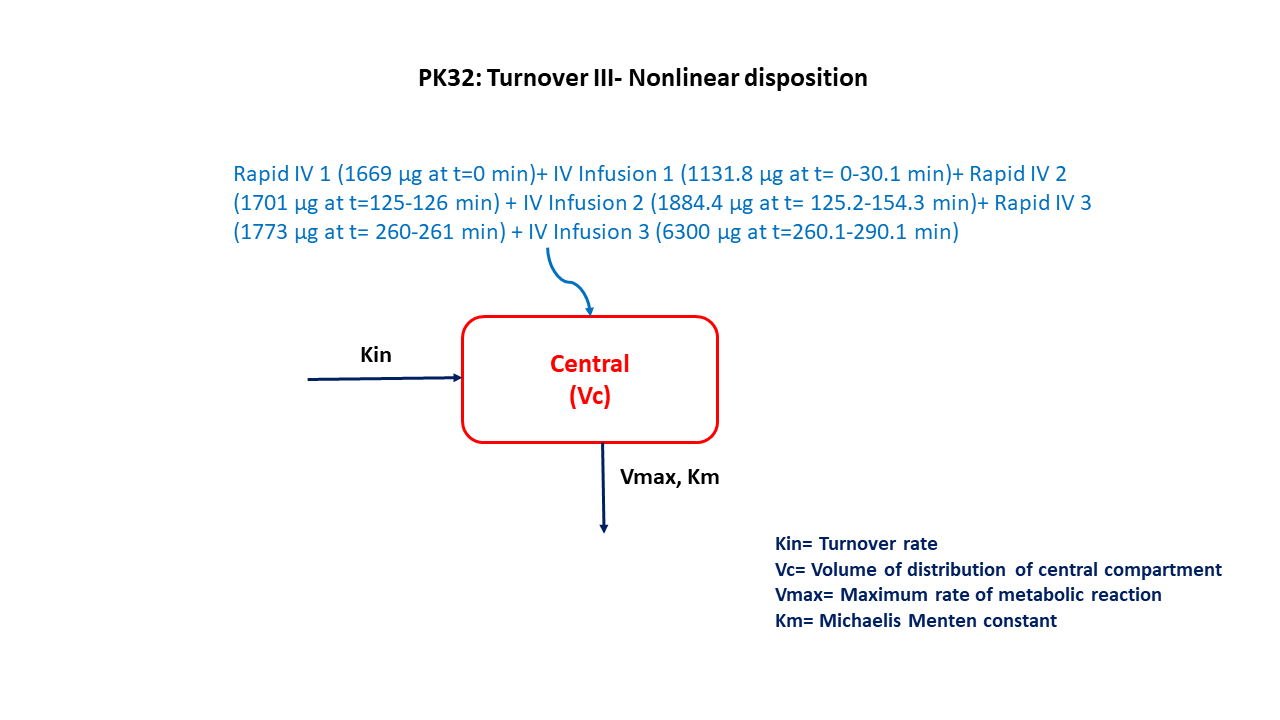
4 Libraries
Call the required libraries to get started.
5 Model
One compartment model for an endogenous compound with non-linear disposition.
pk_32 = @model begin
@metadata begin
desc = "Non-linear Elimination Model"
timeu = u"minute"
end
@param begin
"""
Volume of Central Compartment (L)
"""
tvvc ∈ RealDomain(lower = 0)
"""
Maximum metabolic capacity (μg/min)
"""
tvvmax ∈ RealDomain(lower = 0)
"""
Michaelis-Menten constant (μg/L)
"""
tvkm ∈ RealDomain(lower = 0)
"""
Rate of synthesis (μg/min)
"""
tvkin ∈ RealDomain(lower = 0)
"""
Proportional RUV
"""
σ²_prop ∈ RealDomain(lower = 0)
end
@pre begin
Vc = tvvc
Vmax = tvvmax
Km = tvkm
Kin = tvkin
#CL = Vmax/(Km+(Central/Vc))
end
@init begin
Central = Kin / ((Vmax / Km) / Vc)
end
@dynamics begin
Central' = Kin - (Vmax / (Km + Central / Vc)) * (Central / Vc)
end
@derived begin
cp = @. Central / Vc
"""
Observed Concentration (μg/L)
"""
dv ~ @. Normal(cp, sqrt(cp^2 * σ²_prop))
end
endPumasModel
Parameters: tvvc, tvvmax, tvkm, tvkin, σ²_prop
Random effects:
Covariates:
Dynamical system variables: Central
Dynamical system type: Nonlinear ODE
Derived: cp, dv
Observed: cp, dv6 Parameters
The parameters are as given below.
Vc- Volume of Central Compartment (L)Vmax- Maximum metabolic capacity (μg/min)Km- Michaelis-menten constant (μg/L)Kin- Rate of synthesis, Turnover rate (μg/min)σ- Residual error
These are the initial estimates we will be using in this model exercise. Note that tv represents the typical value for parameters.
param =
(; tvvc = 5.94952, tvvmax = 361.502, tvkm = 507.873, tvkin = 14.9684, σ²_prop = 0.05)7 Dosage Regimen
DosageRegimen - Three sets of rapid intravenous infusions followed by a slow intravenous infusion are defined and coded as follows:
- IV bolus of 1669 μg (Time = 0 min) followed by IV infusion of 1131.8 μg (Time = 0-30.1 min)
- IV infusion of 1701 μg (Time = 0-30.1 min) followed by IV infusion of 1884.4 μg (Time = 125.2-154.3 min)
- IV infusion of 1773 μg (Time = 260-261 min) followed by IV infusion of 6300 μg (Time = 260.1-290.1 min)
IVinfRapid = DosageRegimen(
[1669, 1701, 1733];
time = [0, 125, 260],
cmt = [1, 1, 1],
duration = [0, 1, 1],
)| Row | time | cmt | amt | evid | ii | addl | rate | duration | ss | route |
|---|---|---|---|---|---|---|---|---|---|---|
| Float64 | Int64 | Float64 | Int8 | Float64 | Int64 | Float64 | Float64 | Int8 | NCA.Route | |
| 1 | 0.0 | 1 | 1669.0 | 1 | 0.0 | 0 | 0.0 | 0.0 | 0 | NullRoute |
| 2 | 125.0 | 1 | 1701.0 | 1 | 0.0 | 0 | 1701.0 | 1.0 | 0 | NullRoute |
| 3 | 260.0 | 1 | 1733.0 | 1 | 0.0 | 0 | 1733.0 | 1.0 | 0 | NullRoute |
IVinfSlow = DosageRegimen(
[1131.8, 1884.4, 6300];
time = [0, 125.2, 260.1],
cmt = [1, 1, 1],
duration = [30.1, 29.1, 30],
)| Row | time | cmt | amt | evid | ii | addl | rate | duration | ss | route |
|---|---|---|---|---|---|---|---|---|---|---|
| Float64 | Int64 | Float64 | Int8 | Float64 | Int64 | Float64 | Float64 | Int8 | NCA.Route | |
| 1 | 0.0 | 1 | 1131.8 | 1 | 0.0 | 0 | 37.6013 | 30.1 | 0 | NullRoute |
| 2 | 125.2 | 1 | 1884.4 | 1 | 0.0 | 0 | 64.756 | 29.1 | 0 | NullRoute |
| 3 | 260.1 | 1 | 6300.0 | 1 | 0.0 | 0 | 210.0 | 30.0 | 0 | NullRoute |
This is how to establish the dosing regimen:
DR = DosageRegimen(IVinfRapid, IVinfSlow)| Row | time | cmt | amt | evid | ii | addl | rate | duration | ss | route |
|---|---|---|---|---|---|---|---|---|---|---|
| Float64 | Int64 | Float64 | Int8 | Float64 | Int64 | Float64 | Float64 | Int8 | NCA.Route | |
| 1 | 0.0 | 1 | 1669.0 | 1 | 0.0 | 0 | 0.0 | 0.0 | 0 | NullRoute |
| 2 | 0.0 | 1 | 1131.8 | 1 | 0.0 | 0 | 37.6013 | 30.1 | 0 | NullRoute |
| 3 | 125.0 | 1 | 1701.0 | 1 | 0.0 | 0 | 1701.0 | 1.0 | 0 | NullRoute |
| 4 | 125.2 | 1 | 1884.4 | 1 | 0.0 | 0 | 64.756 | 29.1 | 0 | NullRoute |
| 5 | 260.0 | 1 | 1733.0 | 1 | 0.0 | 0 | 1733.0 | 1.0 | 0 | NullRoute |
| 6 | 260.1 | 1 | 6300.0 | 1 | 0.0 | 0 | 210.0 | 30.0 | 0 | NullRoute |
This is how to create the single subject undergoing the dosing regimen above.
sub1 = Subject(; id = 1, events = DR)Subject
ID: 1
Events: 68 Simulation
To simulate plasma concentration for a single subject with the specific observation time points for a given dosage regimen DR.
The Random.seed! function is included here for purposes of reproducibility of the simulation in this tutorial. Specification of a seed value would not be required in a Pumas workflow that is estimating model parameters.
Random.seed!(123)sim = simobs(pk_32, sub1, param, obstimes = 0:0.01:450)SimulatedObservations
Simulated variables: cp, dv
Time: 0.0:0.01:450.09 Visualization
From the plot, the multiple infusions can be witnessed through the presence of multiple peaks at different time points.
@chain DataFrame(sim) begin
dropmissing(:cp)
data(_) *
mapping(:time => "Time (min)", :cp => "Concentration (μg/L)") *
visual(Lines; linewidth = 4)
draw(; figure = (; fontsize = 22), axis = (; xticks = 0:50:450))
end10 Population Simulation
This block updates the parameters of the model to increase intersubject variability in parameters and defines timepoints for the prediction of concentrations. The results are written to a CSV file.
par = (tvvc = 5.94952, tvvmax = 361.502, tvkm = 507.873, tvkin = 14.9684, σ = 0.05)
IVinfRapid = DosageRegimen(
[1669, 1701, 1733];
time = [0, 125, 260],
cmt = [1, 1, 1],
duration = [0, 1, 1],
)
IVinfSlow = DosageRegimen(
[1131.8, 1884.4, 6300];
time = [0, 125.2, 260.1],
cmt = [1, 1, 1],
duration = [30.1, 29.1, 30],
)
DR = DosageRegimen([IVinfRapid, IVinfSlow])
pop = map(i -> Subject(id = i, events = DR), 1:85)
Random.seed!(1234)
sim_pop = simobs(
pk_32,
pop,
param,
obstimes = [
0,
2.23,
4.2,
6.05,
8.03,
10,
15,
20,
25,
30,
32,
34.1,
36.1,
38.1,
40.1,
42,
45.1,
50,
55,
60,
70,
80,
90.2,
100,
110,
120,
122.8,
127,
129,
131,
133,
135,
140,
145.1,
150,
154,
156,
158,
160,
162,
164,
166,
169,
174,
179,
186.8,
218,
249,
250,
255,
262.2,
264.2,
265.9,
268,
270,
275.1,
280,
285,
290,
292,
294.1,
296.2,
298.1,
300,
302.4,
305.2,
310.1,
315.2,
320,
350.1,
380,
400,
450,
],
)
df_sim = DataFrame(sim_pop)
#CSV.write("pk_32.csv", df_sim)With the CSV.write function, you can input the name of the DataFrame (df_sim) and the file name of your choice (pk_32.csv) to save the file to your local directory or repository.
11 Conclusion
Constructing a model for multiple infusions with non-linear disposition involves:
- understanding the process of how the drug is passed through the system,
- translating processes into ODEs using Pumas, and
- simulating the model in a single patient for evaluation.