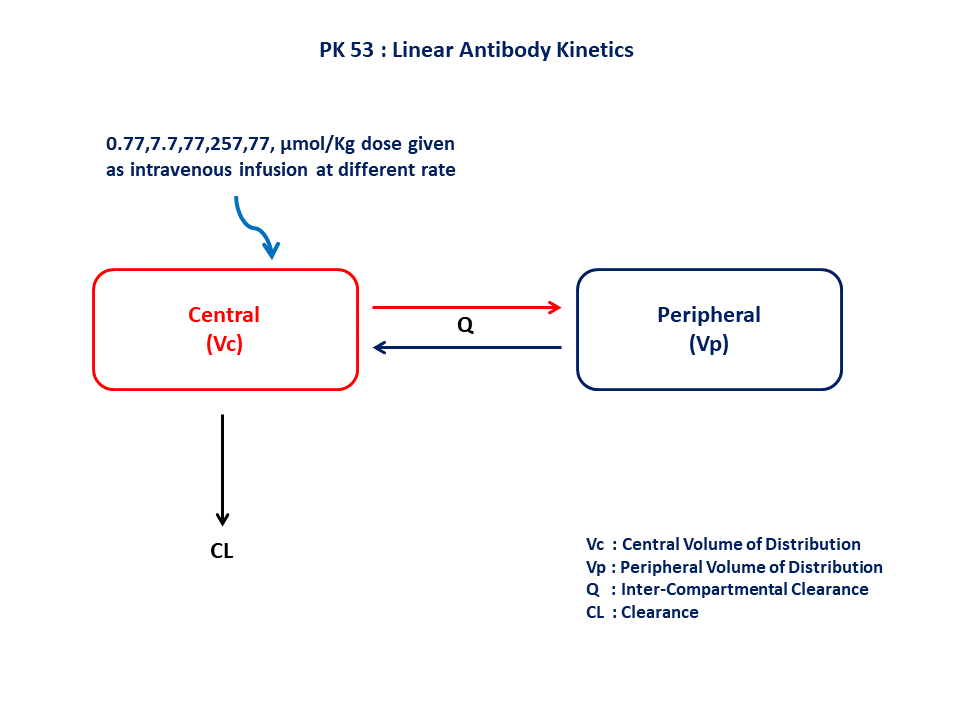
PK53 - Linear antibody kinetics of a two compartment turnover model

1 Background

  • Structural model - Two compartment model
  • Route of administration - Intravenous infusion
  • Dosage Regimen - 0.77, 7.7, 77, 257, and 771 μmol/kg dose given as an intravenous infusion
  • Number of Subjects - 1 (Monkey)

PK53 Model Graphic

2 Learning Outcome

This exercise demonstrates simulating linear antibody kinetics of different doses of an IV infusion from a two compartment turnover model.

3 Objectives

To build a two-compartment turnover model to characterize linear antibody kinetics, simulate the model for a single subject given different IV dosage regimens, and subsequently perform a simulation for a population.

4 Libraries

Load the necessary libraries.

using PumasUtilities
using Random
using Pumas
using CairoMakie
using AlgebraOfGraphics
using CSV
using DataFramesMeta
using Dates

5 Model Definition

Note the expression of the model parameters with helpful comments. The model is expressed with differential equations. Residual variability is a proportional error model.

In this model, we administer the dose in the central compartment.

pk_53 = @model begin
    @metadata begin
        desc = "Two Compartment Model"
        timeu = u"hr"
    end

    @param begin
        """
        Volume of Central Compartment (L/kg)
        """
        tvvc ∈ RealDomain(lower = 0)
        """
        Volume of Peripheral Compartment (L/kg)
        """
        tvvp ∈ RealDomain(lower = 0)
        """
        Clearance (L/hr/kg)
        """
        tvcl ∈ RealDomain(lower = 0)
        """
        Intercompartmental CLearance (L/hr/kg)
        """
        tvq ∈ RealDomain(lower = 0)
        Ω ∈ PDiagDomain(4)
        """
        Proportional RUV
        """
        σ²_prop ∈ RealDomain(lower = 0)
    end

    @random begin
        η ~ MvNormal(Ω)
    end

    @pre begin
        Vc = tvvc * exp(η[1])
        Vp = tvvp * exp(η[2])
        CL = tvcl * exp(η[3])
        Q = tvq * exp(η[4])
    end

    @dynamics begin
        Central' = -(Q / Vc) * Central + (Q / Vp) * Peripheral - (CL / Vc) * Central
        Peripheral' = (Q / Vc) * Central - (Q / Vp) * Peripheral
    end

    @derived begin
        cp = @. Central / Vc
        """
        Observed Concentration (μM)
        """
        dv ~ @. Normal(cp, sqrt(cp^2 * σ²_prop))
    end
end
PumasModel
  Parameters: tvvc, tvvp, tvcl, tvq, Ω, σ²_prop
  Random effects: η
  Covariates:
  Dynamical system variables: Central, Peripheral
  Dynamical system type: Nonlinear ODE
  Derived: cp, dv
  Observed: cp, dv

6 Initial Estimates of Model Parameters

The model parameters for simulation are the following. Note that tv represents the typical value for parameters.

  • Cl - Clearance (L/hr/kg)
  • Vc - Volume of Central Compartment (L/kg)
  • Vp - Volume of Peripheral Compartment (L/kg)
  • Q - Intercompartmental Clearance (L/hr/kg)
  • Ω - Between Subject Variability
  • σ - Residual error
param = (;
    tvvc = 2.139,
    tvvp = 1.5858,
    tvcl = 0.00541,
    tvq = 0.01640,
    Ω = Diagonal([0.01, 0.01, 0.01, 0.01]),
    σ²_prop = 0.04,
)

7 Dosage Regimen

  • Dose 1: 0.77 μmol/kg given as an IV-infusion at time = 0
  • Dose 2: 7.7 μmol/kg given as an IV-infusion at time = 72.17
  • Dose 3: 77 μmol/kg given as an IV-infusion at time = 144.17
  • Dose 4: 257 μmol/kg given as an IV-infusion at time = 216.6
  • Dose 5: 771 μmol/kg given as an IV-infusion at time = 288.52
ev1 = DosageRegimen(0.77, time = 0, cmt = 1, duration = 0.416667)
1×10 DataFrame
Row time cmt amt evid ii addl rate duration ss route
Float64 Int64 Float64 Int8 Float64 Int64 Float64 Float64 Int8 NCA.Route
1 0.0 1 0.77 1 0.0 0 1.848 0.416667 0 NullRoute 
ev2 = DosageRegimen(7.7, time = 72.17, cmt = 1, duration = 0.5)
1×10 DataFrame
Row time cmt amt evid ii addl rate duration ss route
Float64 Int64 Float64 Int8 Float64 Int64 Float64 Float64 Int8 NCA.Route
1 72.17 1 7.7 1 0.0 0 15.4 0.5 0 NullRoute 
ev3 = DosageRegimen(77, time = 144.17, cmt = 1, duration = 0.5)
1×10 DataFrame
Row time cmt amt evid ii addl rate duration ss route
Float64 Int64 Float64 Int8 Float64 Int64 Float64 Float64 Int8 NCA.Route
1 144.17 1 77.0 1 0.0 0 154.0 0.5 0 NullRoute 
ev4 = DosageRegimen(257, time = 216.6, cmt = 1, duration = 0.4)
1×10 DataFrame
Row time cmt amt evid ii addl rate duration ss route
Float64 Int64 Float64 Int8 Float64 Int64 Float64 Float64 Int8 NCA.Route
1 216.6 1 257.0 1 0.0 0 642.5 0.4 0 NullRoute 
ev5 = DosageRegimen(771, time = 288.52, cmt = 1, duration = 0.5)
1×10 DataFrame
Row time cmt amt evid ii addl rate duration ss route
Float64 Int64 Float64 Int8 Float64 Int64 Float64 Float64 Int8 NCA.Route
1 288.52 1 771.0 1 0.0 0 1542.0 0.5 0 NullRoute 
ev = DosageRegimen(ev1, ev2, ev3, ev4, ev5)
5×10 DataFrame
Row time cmt amt evid ii addl rate duration ss route
Float64 Int64 Float64 Int8 Float64 Int64 Float64 Float64 Int8 NCA.Route
1 0.0 1 0.77 1 0.0 0 1.848 0.416667 0 NullRoute
2 72.17 1 7.7 1 0.0 0 15.4 0.5 0 NullRoute
3 144.17 1 77.0 1 0.0 0 154.0 0.5 0 NullRoute
4 216.6 1 257.0 1 0.0 0 642.5 0.4 0 NullRoute
5 288.52 1 771.0 1 0.0 0 1542.0 0.5 0 NullRoute

8 Single-individual that receives the defined dose

sub1 = Subject(id = 1, events = ev)
Subject
  ID: 1
  Events: 5

9 Single-Subject Simulation

Simulate for plasma concentration with the specific observation time points after the intravenous administration.

Initialize the random number generator with a seed for reproducibility of the simulation.

Random.seed!(123)

Define the timepoints at which concentration values will be simulated.

sim_sub1 = simobs(pk_53, sub1, param, obstimes = 0.01:0.01:2000)
SimulatedObservations
  Simulated variables: cp, dv
  Time: 0.01:0.01:2000.0
df1 = DataFrame(sim_sub1)
first(df1, 5)
5×24 DataFrame
Row id time cp dv evid amt cmt rate duration ss ii route tad dosenum Central Peripheral Vc Vp CL Q η_1 η_2 η_3 η_4
String Float64 Float64? Float64? Int64 Float64? Symbol? Float64? Float64? Int8? Float64? NCA.Route? Float64 Int64 Float64? Float64? Float64? Float64? Float64? Float64? Float64 Float64 Float64 Float64
1 1 0.0 missing missing 1 0.77 Central 1.848 0.416667 0 0.0 NullRoute 0.0 1 missing missing 2.00524 1.36994 0.00459923 0.0160469 -0.0645731 -0.146325 -0.16236 -0.0217665
2 1 0.01 0.00921536 0.0101226 0 0.0 missing 0.0 0.0 0 0.0 missing 0.01 1 0.018479 7.39373e-7 2.00524 1.36994 0.00459923 0.0160469 -0.0645731 -0.146325 -0.16236 -0.0217665
3 1 0.02 0.0184298 0.0220456 0 0.0 missing 0.0 0.0 0 0.0 missing 0.02 1 0.0369562 2.95727e-6 2.00524 1.36994 0.00459923 0.0160469 -0.0645731 -0.146325 -0.16236 -0.0217665
4 1 0.03 0.0276432 0.0280853 0 0.0 missing 0.0 0.0 0 0.0 missing 0.03 1 0.0554314 6.65338e-6 2.00524 1.36994 0.00459923 0.0160469 -0.0645731 -0.146325 -0.16236 -0.0217665
5 1 0.04 0.0368557 0.0482746 0 0.0 missing 0.0 0.0 0 0.0 missing 0.04 1 0.0739047 1.18274e-5 2.00524 1.36994 0.00459923 0.0160469 -0.0645731 -0.146325 -0.16236 -0.0217665

10 Visualize Results

@chain DataFrame(sim_sub1) begin
    dropmissing(:cp)
    data(_) *
    mapping(:time => "Time (hours)", :cp => "Concentration (μM)") *
    visual(Lines; linewidth = 4)
    draw(;
        figure = (; fontsize = 22),
        axis = (;
            yscale = log10,
            ytickformat = i -> (@. string(round(i; digits = 1))),
            xticks = 0:200:2000,
        ),
    )
end

11 Population Simulation

We perform a population simulation with 48 participants, and simulate concentration values for 72 hours following 6 doses administered every 8 hours.

This code demonstrates how to write the simulated concentrations to a comma separated file (.csv).

par = (;
    tvvc = 2.139,
    tvvp = 1.5858,
    tvcl = 0.0054,
    tvq = 0.01653,
    Ω = Diagonal([0.045, 0.024, 0.012, 0.0224]),
    σ²_prop = 0.04,
)
ev = DosageRegimen(ev1, ev2, ev3, ev4, ev5)
pop = map(i -> Subject(id = i, events = ev), 1:50)

Random.seed!(1234)
sim_pop = simobs(
    pk_53,
    pop,
    par,
    obstimes = [
        72.67,
        74.17,
        78.17,
        84.17,
        96.17,
        120.17,
        144.17,
        144.67,
        146.17,
        150.17,
        156.17,
        168.17,
        192.17,
        216.17,
        217,
        218.5,
        222.5,
        228.5,
        240.5,
        264.5,
        288.5,
        289.02,
        290.5,
        294.5,
        300.5,
        312.5,
        336.5,
        360.5,
        483.92,
        651.25,
        983.92,
        1751.92,
    ],
)

pkdata_53_sim = DataFrame(sim_pop)
#CSV.write("pk_53_sim.csv", pkdata_53_sim)

12 Conclusion

This tutorial showed how to build a two compartment turnover model to characterize linear antibody kinetics and perform a single subject and a population simulation.