using Random
using Pumas
using PumasUtilities
using AlgebraOfGraphics
using CairoMakie
using CSV
using DataFramesMeta
using Dates
PK27 - Allometry - Elementary & Complex Dedrick plot
1 Background
- Structural model - Target Mediated Drug Disposition Model (TMDD)
- Route of administration - IV-Bolus
- Dosage Regimen - 1.5, 5, 15, 45 mg/kg administered after a complete washout
- Number of Subjects - 4
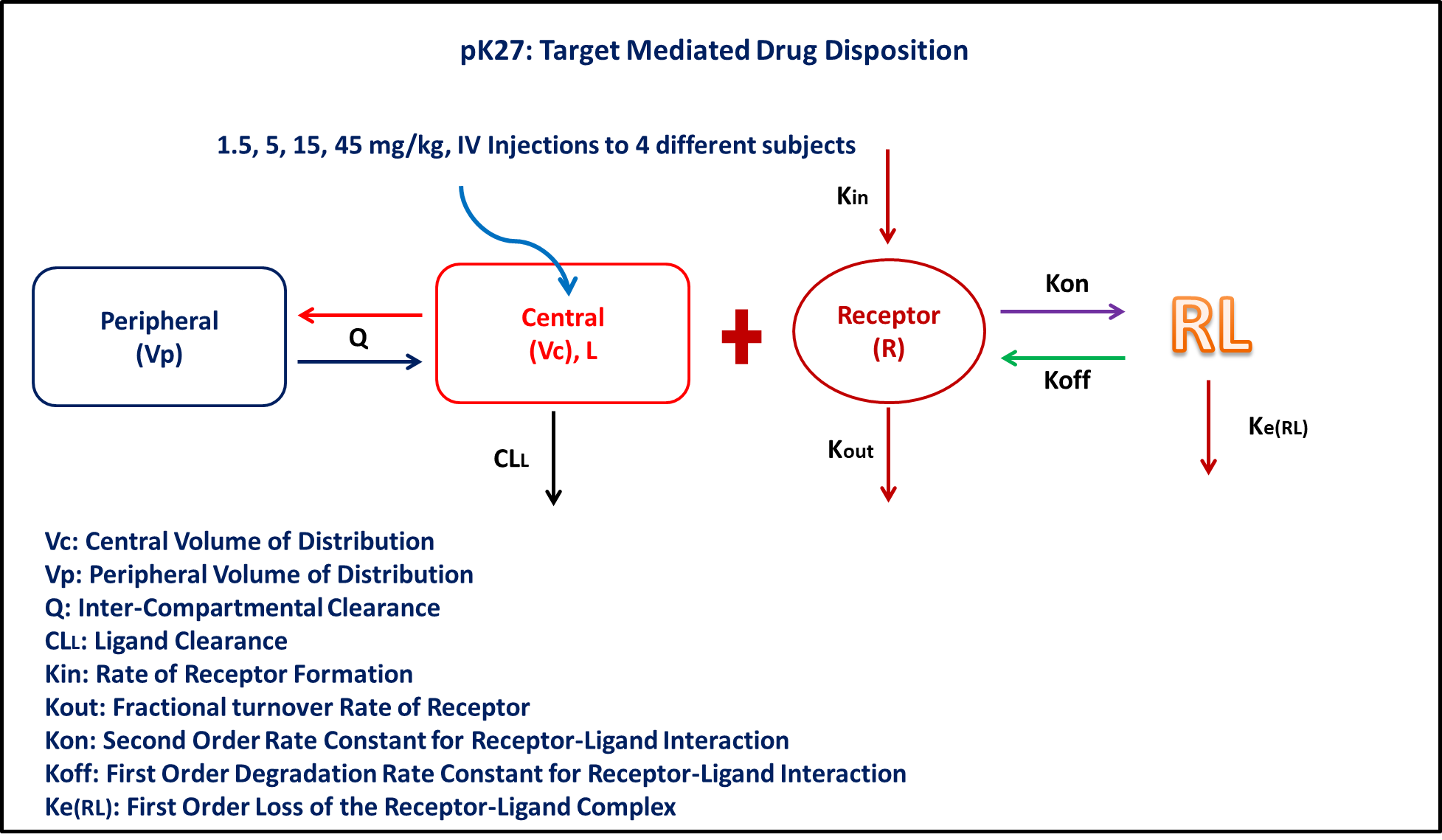
2 Learning Outcome
- To fit a full TMDD model with data from only ligand, ligand and target, target and ligand-target complex
- Write a differential equation for a full TMDD model
3 Objective
The objective of this exercise is to simulate from a TMDD model
4 Libraries
Call the necessary libraries to get started
5 Model
pk_27 = @model begin
@metadata begin
desc = "Target Mediated Drug Disposition Model"
timeu = u"hr"
end
@param begin
"""
Clearance of central compartment (L/kg/hr)
"""
tvcl ∈ RealDomain(lower = 0)
"""
Second order on rate of ligand (L/mg/hr)
"""
tvkon ∈ RealDomain(lower = 0)
"""
First order off rate of ligand (1/hr)
"""
tvkoff ∈ RealDomain(lower = 0)
"""
Volume of Peripheral Compartment (L/kg)
"""
tvvp ∈ RealDomain(lower = 0)
"""
Inter-compartmental clearance (L/kg/hr)
"""
tvq ∈ RealDomain(lower = 0)
"""
Zero order receptor synthesis process (mg/L/hr)
"""
tvkin ∈ RealDomain(lower = 0)
"""
First order receptor degeneration process (1/hr)
"""
tvkout ∈ RealDomain(lower = 0)
"""
First order elimination of complex (1/hr)
"""
tvkerl ∈ RealDomain(lower = 0)
"""
Volume of Central Compartment (L/kg)
"""
tvvc ∈ RealDomain(lower = 0)
Ω ∈ PDiagDomain(9)
"""
Proportional RUV - Plasma
"""
σ²_prop_cp ∈ RealDomain(lower = 0)
"""
Proportional RUV - Receptor
"""
σ²_prop_rec ∈ RealDomain(lower = 0)
"""
Proportional RUV - Complex
"""
σ²_prop_com ∈ RealDomain(lower = 0)
end
@random begin
η ~ MvNormal(Ω)
end
@pre begin
Cl = tvcl * exp(η[1])
Kon = tvkon * exp(η[2])
Koff = tvkoff * exp(η[3])
Vp = tvvp * exp(η[4])
Q = tvq * exp(η[5])
Kin = tvkin * exp(η[6])
Kout = tvkout * exp(η[7])
Kerl = tvkerl * exp(η[8])
Vc = tvvc * exp(η[9])
end
@dosecontrol begin
Vc_ := tvvc * exp(η[9])
bioav = (Central = 1 / Vc_,)
end
@init begin
Receptor = Kin / Kout
end
@dynamics begin
Central' =
-(Cl / Vc) * Central - (Q / Vc) * Central + (Q / Vp) * Peripheral -
Kon * Receptor * Central + Koff * Complex
Peripheral' = (Q / Vc) * Central - (Q / Vp) * Peripheral
Receptor' = Kin - Kout * Receptor - Kon * Receptor * Central + Koff * Complex
Complex' = Kon * Receptor * Central - Koff * Complex - Kerl * Complex
end
@derived begin
cp = @. Central
"""
Observed Concentration - Plasma (mg/L)
"""
dv_cp = @. Normal(cp, sqrt(cp^2 * σ²_prop_cp))
rec = @. Receptor
"""
Observed Concentration - Receptor (mg/L)
"""
dv_rec = @. Normal(rec, sqrt(rec^2 * σ²_prop_rec))
com = @. Complex
"""
Observed Concentration - Complex (mg/L)
"""
dv_com = @. Normal(com, sqrt(com^2 * σ²_prop_com))
end
endPumasModel
Parameters: tvcl, tvkon, tvkoff, tvvp, tvq, tvkin, tvkout, tvkerl, tvvc, Ω, σ²_prop_cp, σ²_prop_rec, σ²_prop_com
Random effects: η
Covariates:
Dynamical system variables: Central, Peripheral, Receptor, Complex
Dynamical system type: Nonlinear ODE
Derived: cp, dv_cp, rec, dv_rec, com, dv_com
Observed: cp, dv_cp, rec, dv_rec, com, dv_com6 Parameters
The parameters are as given below. tv represents the typical value for parameters.
Cl- Clearance of central compartment (L/kg/hr)Kon- Second order on rate of ligand (L/mg/hr)Koff- First order off rate of ligand (1/hr)Vp- Volume of Peripheral Compartment (L/kg)Q- Inter-compartmental clearance (L/kg/hr)Kin- Zero order receptor synthesis process (mg/L/hr)Kout- First order receptor degeneration process (1/hr)Kerl- First order elimination of complex (1/hr)Vc- Volume of Central Compartment (L/kg)
param = (
tvcl = 0.001,
tvkon = 0.096,
tvkoff = 0.001,
tvvp = 0.100,
tvq = 0.003,
tvkin = 0.11,
tvkout = 0.0089,
tvkerl = 0.003,
tvvc = 0.05,
Ω = Diagonal([0.04, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04]),
σ²_prop_cp = 0.02,
σ²_prop_rec = 0.012,
σ²_prop_com = 0.015,
)7 Dosage Regimen
- Single dose of 1.5 mg/kg was administered as IV-Bolus at
time=0 - Single dose of 5 mg/kg was administered as IV-Bolus at
time=0 - Single dose of 15 mg/kg was administered as IV-Bolus at
time=0 - Single dose of 45 mg/kg was administered as IV-Bolus at
time=0
dose = [1.5, 5, 15, 45]ids = ["1.5 mg/kg", "5 mg/kg", "15 mg/kg", "45 mg/kg"]dose_ind(x) = DosageRegimen(dose[x], time = 0, cmt = 1)pop4_sub = map(i -> Subject(id = ids[i], events = dose_ind(i)), 1:length(ids))Population
Subjects: 4
Observations: 8 Simulation
Random.seed!(123)The random effects are zero’ed out since we are simulating means
zfx = zero_randeffs(pk_27, pop4_sub, param)4-element Vector{@NamedTuple{η::Vector{Float64}}}:
(η = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],)
(η = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],)
(η = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],)
(η = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],)sim_pop4 = simobs(pk_27, pop4_sub, param, zfx, obstimes = 0.1:1:500)Simulated population (Vector{<:Subject})
Simulated subjects: 4
Simulated variables: cp, dv_cp, rec, dv_rec, com, dv_com9 Visualization
df27 = @chain DataFrame(sim_pop4) begin
dropmissing([:cp, :rec, :com])
endfig = Figure(; fontsize = 32, resolution = (1200, 1200))
ytickformater(ticks) = @. string(round(ticks; digits = 1))
gridpos = fig[1, 1]
plt1 =
data(df27) *
mapping(
:time => "Time (days)",
:cp => "PK27 Concentrations (mg/L)",
color = :id => nonnumeric => "Doses",
) *
visual(Lines, linewidth = 6)
draw!(
gridpos,
plt1;
axis = (;
title = "Ligand",
yscale = log10,
yticks = map(i -> 10.0^i, -2:2),
ytickformat = ytickformater,
xticks = 0:100:500,
),
)
gridpos = fig[1, 2]
plt2 =
data(df27) *
mapping(
:time => "Time (days)",
:rec => "PK27 Concentrations (mg/L)",
color = :id => nonnumeric => "Doses",
) *
visual(Lines, linewidth = 6)
draw!(
gridpos,
plt2;
axis = (;
title = "Receptor",
yscale = log10,
yticks = map(i -> 10.0^i, -2:1),
ytickformat = ytickformater,
xticks = 0:100:500,
),
)
gridpos = fig[2, 1]
plt3 =
data(df27) *
mapping(
:time => "Time (days)",
:com => "PK27 Concentrations (mg/L)",
color = :id => nonnumeric => "Doses",
) *
visual(Lines, linewidth = 6)
p3 = draw!(
gridpos,
plt3;
axis = (;
title = "Complex",
yscale = log10,
yticks = map(i -> 10.0^i, 0.6:0.2:1.4),
ytickformat = ytickformater,
xticks = 0:100:500,
),
)
gridpos = fig[2, 2]
legend!(
gridpos,
p3;
linewidth = 8,
tellwidth = false,
halign = :right,
valign = :center,
margin = (10, 10, 10, 10),
)
fig┌ Warning: Found `resolution` in the theme when creating a `Scene`. The `resolution` keyword for `Scene`s and `Figure`s has been deprecated. Use `Figure(; size = ...` or `Scene(; size = ...)` instead, which better reflects that this is a unitless size and not a pixel resolution. The key could also come from `set_theme!` calls or related theming functions. └ @ Makie ~/run/_work/PumasTutorials.jl/PumasTutorials.jl/custom_julia_depot/packages/Makie/FUAHr/src/scenes.jl:238
10 Population simulation
par = (
tvcl = 0.001,
tvkon = 0.096,
tvkoff = 0.001,
tvvp = 0.100,
tvq = 0.003,
tvkin = 0.11,
tvkout = 0.0089,
tvkerl = 0.003,
tvvc = 0.05,
Ω = Diagonal([0.09, 0.04, 0.0125, 0.04, 0.0326, 0.0525, 0.0124, 0.0111, 0.0234]),
σ²_prop_cp = 0.025,
σ²_prop_rec = 0.03,
σ²_prop_com = 0.04,
)
ev1 = DosageRegimen(1.5, cmt = 1, time = 0)
pop1 = map(i -> Subject(id = i, events = ev1), 1:20)
ev2 = DosageRegimen(5, cmt = 1, time = 0)
pop2 = map(i -> Subject(id = i, events = ev2), 21:40)
ev3 = DosageRegimen(15, cmt = 1, time = 0)
pop3 = map(i -> Subject(id = i, events = ev3), 41:60)
ev4 = DosageRegimen(45, cmt = 1, time = 0)
pop4 = map(i -> Subject(id = i, events = ev4), 61:80)
pop = [pop1; pop2; pop3; pop4]
## Simulation
Random.seed!(1234)
sim_pop = simobs(pk_27, pop, par, obstimes = [0.1, 1, 10, 24, 72, 120, 168, 240, 360, 499])
sim_plot(sim_pop)
df_sim = DataFrame(sim_pop);
#CSV.write("pk_27.csv", df_sim)