PK43 - Multiple Absorption Routes

1 Learning Outcome

In this exercise, we will be looking at multiple absorption routes and how a model helps in understanding the absorption of sublingually administered doses, partly from the buccal cavity and partly from the gastrointestinal (GI) tract.

2 Objectives

In this model, you will learn how to write a differential equation model for a drug that is partly absorbed from the buccal and partly from the GI and simulate for a single subject.

3 Background

Before constructing a model, it is important to establish the process the model will follow and a scenario for the simulation.

Below is the scenario for this tutorial:

  • Structural model - 1 compartment linear elimination with first order absorption
  • Route of administration - Sublingual
  • Dosage Regimen - 2 mg Sublingual dose
  • Number of Subjects - 1

This diagram describes how such an administered dose will be handled, which facilitates building the model. 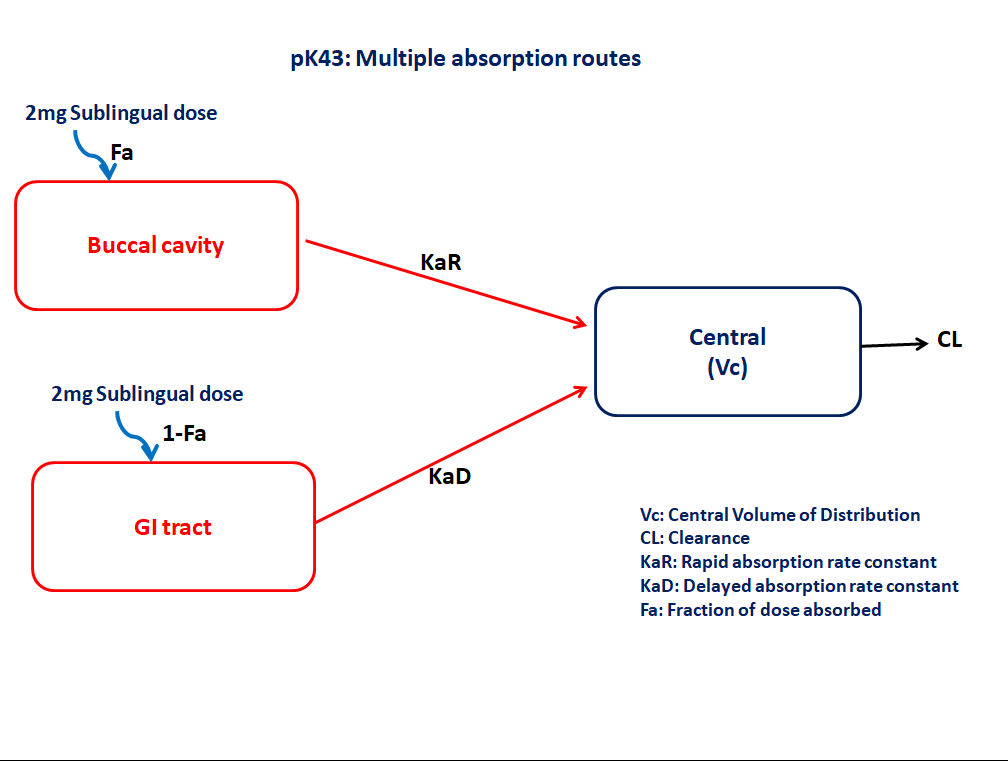PK43 Model Graphic

4 Libraries

Call the required libraries to get started.

using Pumas
using PumasUtilities
using Random
using CairoMakie
using AlgebraOfGraphics
using CSV
using DataFramesMeta

5 Model

In this one compartment model, we administer the dose sublingually at 2 sites. Both sites are accounted for in the @dosecontrol block, including the lag time from the absorption process occurring physiologically in the GI tract.

pk_43 = @model begin
    @metadata begin
        desc = "Multiple Absorption Model"
        timeu = u"hr"
    end

    @param begin
        """
        Absorption rate constant(rapid from buccal) (hr⁻¹)
        """
        tvkar ∈ RealDomain(lower = 0)
        """
        Absorption rate constant(delayed from GI) (hr⁻¹)
        """
        tvkad ∈ RealDomain(lower = 0)
        """
        Volume of Central Compartment (L)
        """
        tvv ∈ RealDomain(lower = 0)
        """
        Lagtime (hr)
        """
        tvlag ∈ RealDomain(lower = 0)
        """
        Fraction of drug absorbed
        """
        tvfa ∈ RealDomain(lower = 0)
        """
        Elimination rate constant (hr⁻¹)
        """
        tvk ∈ RealDomain(lower = 0)
        Ω ∈ PDiagDomain(4)
        """
        Additive RUV
        """
        σ_add ∈ RealDomain(lower = 0)
    end

    @random begin
        η ~ MvNormal(Ω)
    end

    @pre begin
        KaR = tvkar * exp(η[1])
        KaD = tvkad * exp(η[2])
        V = tvv * exp(η[3])
        K = tvk * exp(η[4])
    end

    @dosecontrol begin
        bioav = (Buccal = tvfa, Gi = 1 - tvfa)
        lags = (Gi = tvlag,)
    end

    @dynamics begin
        Buccal' = -KaR * Buccal
        Gi' = -KaD * Gi
        Central' = KaR * Buccal + KaD * Gi - K * Central
    end

    @derived begin
        cp = @. Central / V
        """
        Observed Concentration (mcg/L)
        """
        dv ~ @. Normal(cp, σ_add)
    end
end
PumasModel
  Parameters: tvkar, tvkad, tvv, tvlag, tvfa, tvk, Ω, σ_add
  Random effects: η
  Covariates: 
  Dynamical system variables: Buccal, Gi, Central
  Dynamical system type: Matrix exponential
  Derived: cp, dv
  Observed: cp, dv

6 Parameters

Parameters provided for simulation.

  • Vc - Volume of Central Compartment (L)
  • K - Elimination rate constant (hr⁻¹)
  • Kar - Absorption rate constant(rapid from buccal) (hr⁻¹)
  • Kad - Absorption rate constant(delayed from GI) (hr⁻¹)
  • Fa - Fraction of drug absorbed
  • lags - Lagtime (hr)
  • Ω - Between Subject Variability
  • σ - Residual error

These are the initial estimates we will be using in this model exercise. Note that tv represents the typical value for parameters.

param = (;
    tvkar = 7.62369,
    tvkad = 1.0751,
    tvv = 20.6274,
    tvk = 0.0886931,
    tvfa = 0.515023,
    tvlag = 2.29614,
    Ω = Diagonal([0.01, 0.01, 0.01, 0.01]),
    σ_add = 0.86145,
)

7 Dosage Regimen

To start the simulation process, the dosing regimen specified in the background section must be developed first prior to running a simulation.

The dosage regimen is specified as:

A Single subject receiving a 2 mg dose given orally (absorbed - Sublingually and remaining from the Gut).

This is how to establish the dosing regimen:

ev1 = DosageRegimen(2000; time = 0, cmt = [1, 2])
2×10 DataFrame
Row time cmt amt evid ii addl rate duration ss route
Float64 Int64 Float64 Int8 Float64 Int64 Float64 Float64 Int8 NCA.Route
1 0.0 1 2000.0 1 0.0 0 0.0 0.0 0 NullRoute
2 0.0 2 2000.0 1 0.0 0 0.0 0.0 0 NullRoute

This is how to create the single subject undergoing the dosing regimen above.

sub1 = Subject(; id = 1, events = ev1)
Subject
  ID: 1
  Events: 2

8 Simulation

Let’s simulate plasma concentration with specific observation times after a sublingual dose, considering multiple absorption routes.

Random.seed!()

The Random.seed! function is included here for purposes of reproducibility of the simulation in this tutorial. Specification of a seed value would not be required in a Pumas workflow that is estimating model parameters.

Random.seed!(123)
sim_sub1 = simobs(pk_43, sub1, param, obstimes = 0.00:0.01:24)
SimulatedObservations
  Simulated variables: cp, dv
  Time: 0.0:0.01:24.0

9 Visualization

From the plot below, the concentration can be observed having a varying absorption profile.

@chain DataFrame(sim_sub1) begin
    dropmissing(:cp)
    data(_) *
    mapping(:time => "Time (minutes)", :cp => "Concentration (μg/L)";) *
    visual(Lines; linewidth = 4)
    draw(; figure = (; fontsize = 22), axis = (; xticks = 0:5:25))
end

10 Population Simulation

This block updates the parameters of the model to increase intersubject variability in parameters and defines timepoints for prediction of concentrations. The results are written to a CSV file.

par = (
    tvkar = 7.62369,
    tvkad = 1.0751,
    tvv = 20.6274,
    tvk = 0.0886931,
    tvfa = 0.515023,
    tvlag = 2.29614,
    Ω = Diagonal([0.0635, 0.0125, 0.03651, 0.0198]),
    σ_add = 1.86145,
)

ev1 = DosageRegimen(2000; time = 0, cmt = [1, 2])
pop = map(i -> Subject(id = i, events = ev1), 1:68)

Random.seed!(1234)
sim_pop = simobs(
    pk_43,
    pop,
    par,
    obstimes = [0.1, 0.15, 0.25, 0.5, 0.75, 0.8, 1, 1.25, 1.5, 2, 3, 4, 5, 6, 8, 12, 24],
)

df_sim = DataFrame(sim_pop)
#CSV.write("pk_43.csv", df_sim)
Saving the Simulation Results

With the CSV.write function, you can input the name of the DataFrame (df_sim) and the file name of your choice (pk_43.csv) to save the file to your local directory or repository.

11 Conclusion

Constructing a model with multiple absorption routes involves:

  • understanding the process of how the drug is absorbed and passed through the system,
  • translating the absorption and subsequent processes into ODEs in Pumas, and
  • simulating the model in a single patient for evaluation.