PK49 - Turnover IV - Factor II data in healthy volunteers

1 Background

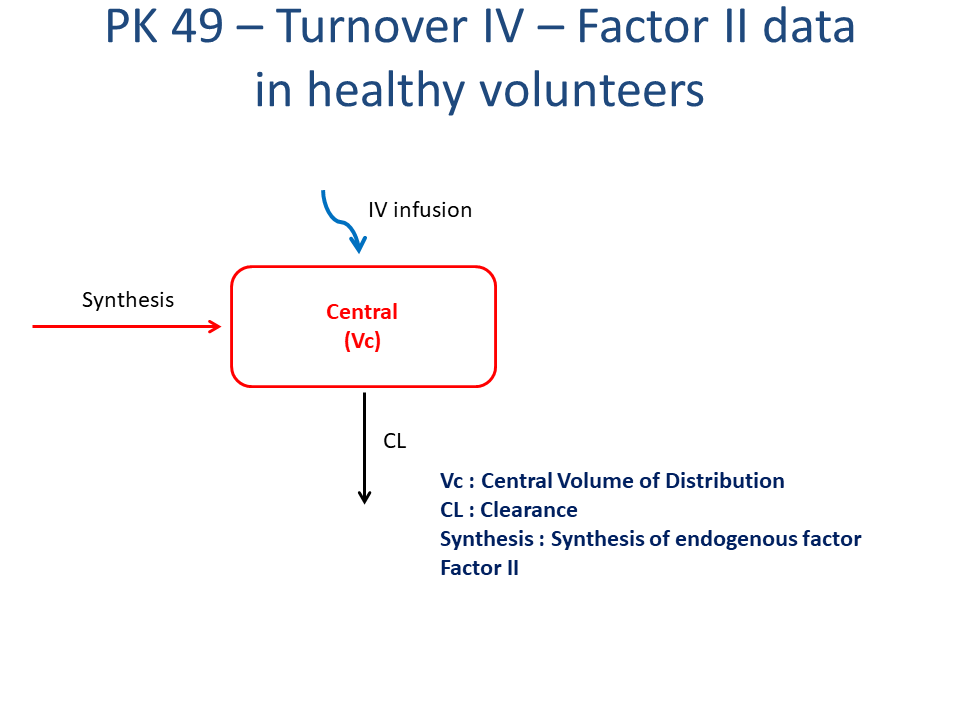
Structural model - One compartment turnover model
Route of administration - Intravenous infusion
Dosage Regimen - 400 mg dose given as a 19 minute constant intravenous infusion
Number of Subjects - 1 (Healthy Volunteer)

2 Learning Outcome

This exercise demonstrates simulating constant IV infusion kinetics from a one compartment turnover model.

3 Objectives

To build one compartment turnover model with constant intravenous infusion and simulate the model for a single subject, and subsequently perform a simulation for a population.

4 Libraries

Load the necessary libraries.

using PumasUtilities
using Random
using Pumas
using CairoMakie
using AlgebraOfGraphics
using CSV
using DataFramesMeta
using Dates

5 Model Definition

Note the expression of the model parameters with helpful comments. The model is expressed with differential equations. Residual variability is an additive error model.

pk_49 = @model begin
    @metadata begin
        desc = "One Compartment Model"
        timeu = u"hr"
    end

    @param begin
        """
        Clearance (L/hr)
        """
        tvcl ∈ RealDomain(lower = 0)
        """
        Volume of Central Compartment (L)
        """
        tvvc ∈ RealDomain(lower = 0)
        """
        Synthesis of endogenous coagulation Factor II (mg/hr)
        """
        tvsynthesis ∈ RealDomain(lower = 0)
        Ω ∈ PDiagDomain(3)
        """
        Additive RUV
        """
        σ_add ∈ RealDomain(lower = 0)
    end

    @random begin
        η ~ MvNormal(Ω)
    end

    @pre begin
        CL = tvcl * exp(η[1])
        Vc = tvvc * exp(η[2])
        Synthesis = tvsynthesis * exp(η[3])
    end

    @init begin
        Central = Synthesis / (CL / Vc) # We add Vc here because we want it in "amount". not conc.
    end

    @dynamics begin
        Central' = Synthesis - (CL / Vc) * Central
    end

    @derived begin
        cp = @. Central / Vc
        """
        Observed Concentration (μg/L)
        """
        dv ~ @. Normal(cp, σ_add)
    end
end

PumasModel
  Parameters: tvcl, tvvc, tvsynthesis, Ω, σ_add
  Random effects: η
  Covariates:
  Dynamical system variables: Central
  Dynamical system type: Matrix exponential
  Derived: cp, dv
  Observed: cp, dv

6 Initial Estimates of Model Parameters

The model parameters for simulation are the following. Note that tv represents the typical value for parameters.

Cl - Clearance (L/hr)
Vc - Volume of Central Compartment (L)
Synthesis - Synthesis of endogenous coagulation Factor II (mg/hr)
Ω - Between Subject Variability
σ - Residual error

param = (;
    tvcl = 0.14204,
    tvvc = 3.59259,
    tvsynthesis = 16.2272,
    Ω = Diagonal([0.01, 0.01, 0.01]),
    σ_add = 2.96,
)

7 Dosage Regimen

Dosage Regimen - 400 mg of an IV-Infusion over a period of 19 minutes in a healthy individual.

ev1 = DosageRegimen(400, cmt = 1, duration = 0.3166)

1×10 DataFrame

Row	time	cmt	amt	evid	ii	addl	rate	duration	ss	route
	Float64	Int64	Float64	Int8	Float64	Int64	Float64	Float64	Int8	NCA.Route
1	0.0	1	400.0	1	0.0	0	1263.42	0.3166	0	NullRoute

8 Single-individual that receives the defined dose

sub1 = Subject(id = 1, events = ev1)

Subject
  ID: 1
  Events: 1

9 Single-Subject Simulation

Simulate for plasma concentration with the specific observation time points after Intravenous administration.

Initialize the random number generator with a seed for reproducibility of the simulation.

Random.seed!(123)

Define the timepoints at which concentration values will be simulated.

sim_sub1 = simobs(
    pk_49,
    sub1,
    param,
    obstimes = [
        0.01,
        0.05,
        0.08,
        0.16,
        0.25,
        0.5,
        1,
        2,
        3,
        4,
        5,
        6,
        7,
        8,
        9,
        12,
        15,
        18,
        24,
        32,
        48,
        72,
        96,
        144,
    ],
)

SimulatedObservations
  Simulated variables: cp, dv
  Time: [0.01, 0.05, 0.08, 0.16, 0.25, 0.5, 1.0, 2.0, 3.0, 4.0  …  9.0, 12.0, 15.0, 18.0, 24.0, 32.0, 48.0, 72.0, 96.0, 144.0]

10 Visualize Results

@chain DataFrame(sim_sub1) begin
    dropmissing(:cp)
    data(_) *
    mapping(:time => "Time (hours)", :cp => "Concentration (μg/L)") *
    visual(Lines; linewidth = 4)
    draw(; figure = (; fontsize = 22), axis = (; xticks = 0:20:160, yticks = 80:20:240))
end

11 Population Simulation

We perform a population simulation with 85 participants.

This code demonstrates how to write the simulated concentrations to a comma separated file (.csv).

par = (;
    tvcl = 0.14204,
    tvvc = 3.59259,
    tvsynthesis = 16.2272,
    Ω = Diagonal([0.04261, 0.025, 0.001]),
    σ_add = 7.9609,
)

ev1 = DosageRegimen(400, cmt = 1, duration = 0.3166)
pop = map(i -> Subject(id = i, events = ev1), 1:85)

Random.seed!(1234)
pop_sim = simobs(
    pk_49,
    pop,
    par,
    obstimes = [
        0.01,
        0.05,
        0.08,
        0.16,
        0.25,
        0.5,
        1,
        2,
        3,
        4,
        5,
        6,
        7,
        8,
        9,
        12,
        15,
        18,
        24,
        32,
        48,
        72,
        96,
        144,
    ],
)

pkdata_49_sim = DataFrame(pop_sim)
#CSV.write("pk_49_sim.csv", pkdata_49_sim)

12 Conclusion

This tutorial showed how to build a one compartment turnover model with constant intravenous infusion and perform a single subject and population simulation.