using Random
using Pumas
using PumasUtilities
using AlgebraOfGraphics
using CairoMakie
using CSV
using DataFramesMeta
using Dates
PK13 - Bolus plus constant rate infusion
1 Background
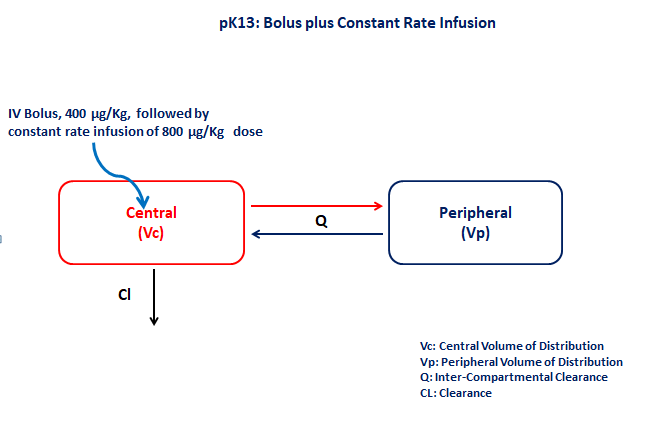
- Structural model - Two compartment model with first order elimination
- Route of administration - IV-Bolus and IV-Infusion given simultaneously
- Dosage Regimen - 400 μg/kg IV-Bolus and 800 μg/kg IV-Infusion for 26 minutes
- Number of Subjects - 1
2 Learning Outcome
- Write the differential equation for a two-compartment model in terms of Clearance and Volume
- Simulate data for a bolus dose followed by a constant rate infusion regimen
- Observe how the administration of a loading dose helps to achieve therapeutic concentrations faster
3 Objective
The objective of this exercise is to simulate data from a bolus followed by a constant rate infusion using a differential equation model.
4 Libraries
Call the necessary libraries to get started
5 Model
The given data follows a two compartment model in which the IV Bolus and IV-Infusion are administered at time=0
pk_13 = @model begin
@metadata begin
desc = "Two Compartment Model"
timeu = u"minute"
end
@param begin
"""
Clearance (L/min/kg)
"""
tvcl ∈ RealDomain(lower = 0)
"""
Volume of Central Compartment (L/kg)
"""
tvvc ∈ RealDomain(lower = 0)
"""
Inter-compartmental Clearance (L/min/kg)
"""
tvq ∈ RealDomain(lower = 0)
"""
Volume of Peripheral Compartment (L/kg)
"""
tvvp ∈ RealDomain(lower = 0)
Ω ∈ PDiagDomain(4)
"""
Proportional RUV
"""
σ²_prop ∈ RealDomain(lower = 0)
"""
Additive RUV
"""
σ²_add ∈ RealDomain(lower = 0)
end
@random begin
η ~ MvNormal(Ω)
end
@pre begin
Cl = tvcl * exp(η[1])
Vc = tvvc * exp(η[2])
Q = tvq * exp(η[3])
Vp = tvvp * exp(η[4])
end
@dynamics begin
Central' = -(Cl / Vc) * Central - (Q / Vc) * Central + (Q / Vp) * Peripheral
Peripheral' = (Q / Vc) * Central - (Q / Vp) * Peripheral
end
@derived begin
cp = @. Central / Vc
"""
Observed Concentrations (μg/L)
"""
dv ~ @. Normal(cp, sqrt((cp * σ²_prop)^2 + σ²_add^2))
end
endPumasModel
Parameters: tvcl, tvvc, tvq, tvvp, Ω, σ²_prop, σ²_add
Random effects: η
Covariates:
Dynamical system variables: Central, Peripheral
Dynamical system type: Matrix exponential
Derived: cp, dv
Observed: cp, dv6 Parameters
Cl- Clearance of central compartment (L/min/kg)Vc- Volume of central compartment (L/kg)Q- Inter-compartmental clearance (L/min/kg)Vp- Volume of peripheral compartment (L/kg)Ω- Between Subject Variabilityσ- Residual Unexplained Variability
param = (
tvcl = 0.344708,
tvvc = 2.8946,
tvq = 0.178392,
tvvp = 2.18368,
Ω = Diagonal([0.04, 0.04, 0.04, 0.04]),
σ²_prop = 0.0571079,
σ²_add = 0.1,
)7 Dosage Regimen
- Single dose of 400 μg/kg given as an IV-Bolus at
time=0 - Single dose of 800 μg/kg given as an IV-Infusion for 26 minutes at
time=0
ev1 = DosageRegimen(400, time = 0, cmt = 1)1×10 DataFrame
| Row | time | cmt | amt | evid | ii | addl | rate | duration | ss | route |
|---|---|---|---|---|---|---|---|---|---|---|
| Float64 | Int64 | Float64 | Int8 | Float64 | Int64 | Float64 | Float64 | Int8 | NCA.Route | |
| 1 | 0.0 | 1 | 400.0 | 1 | 0.0 | 0 | 0.0 | 0.0 | 0 | NullRoute |
ev2 = DosageRegimen(800, time = 0, cmt = 1, rate = 30.769)1×10 DataFrame
| Row | time | cmt | amt | evid | ii | addl | rate | duration | ss | route |
|---|---|---|---|---|---|---|---|---|---|---|
| Float64 | Int64 | Float64 | Int8 | Float64 | Int64 | Float64 | Float64 | Int8 | NCA.Route | |
| 1 | 0.0 | 1 | 800.0 | 1 | 0.0 | 0 | 30.769 | 26.0002 | 0 | NullRoute |
ev3 = DosageRegimen(ev1, ev2)2×10 DataFrame
| Row | time | cmt | amt | evid | ii | addl | rate | duration | ss | route |
|---|---|---|---|---|---|---|---|---|---|---|
| Float64 | Int64 | Float64 | Int8 | Float64 | Int64 | Float64 | Float64 | Int8 | NCA.Route | |
| 1 | 0.0 | 1 | 400.0 | 1 | 0.0 | 0 | 0.0 | 0.0 | 0 | NullRoute |
| 2 | 0.0 | 1 | 800.0 | 1 | 0.0 | 0 | 30.769 | 26.0002 | 0 | NullRoute |
sub1 = Subject(id = 1, events = ev3)Subject
ID: 1
Events: 38 Simulation
We will simulate the plasma concentration at the pre-specified time points.
Random.seed!(123)The random effects are zero’ed out since we are simulating means
zfx = zero_randeffs(pk_13, sub1, param)(η = [0.0, 0.0, 0.0, 0.0],)sim_sub1 = simobs(
pk_13,
sub1,
param,
zfx,
obstimes = [
2,
5,
10,
15,
20,
25,
30,
33,
35,
37,
40,
45,
50,
60,
70,
90,
110,
120,
150,
],
)SimulatedObservations
Simulated variables: cp, dv
Time: [2, 5, 10, 15, 20, 25, 30, 33, 35, 37, 40, 45, 50, 60, 70, 90, 110, 120, 150]9 Visualization
@chain DataFrame(sim_sub1) begin
dropmissing(:cp)
data(_) *
mapping(:time => "Time (min)", :cp => "PK13 Concentration (μg/L)") *
visual(Lines, linewidth = 4)
draw(;
axis = (;
yscale = log10,
xticks = 0:20:160,
ytickformat = x -> string.(round.(x; digits = 1)),
ygridwidth = 3,
yminorticksvisible = true,
yminorgridvisible = true,
yminorticks = IntervalsBetween(10),
),
figure = (; fontsize = 22),
)
endpar = (
tvcl = 0.344708,
tvvc = 2.8946,
tvq = 0.178392,
tvvp = 2.18368,
Ω = Diagonal([0.09, 0.04, 0.0225, 0.0125]),
# tvCMixRatio = 1.00693,
σ²_prop = 0.0571079,
σ²_add = 0.2,
)
ev = DosageRegimen([400, 800], time = 0, cmt = 1, duration = [0, 26])
pop = map(i -> Subject(id = i, events = ev), 1:48)
Random.seed!(1234)
pop_sim = simobs(
pk_13,
pop,
par,
obstimes = [
2,
5,
10,
15,
20,
25,
30,
33,
35,
37,
40,
45,
50,
60,
70,
90,
110,
120,
150,
],
)
sim_plot(pop_sim)
df_sim = DataFrame(pop_sim)
#CSV.write("pk_13.csv", df_sim)