using Random
using Pumas
using PumasUtilities
using CairoMakie
using AlgebraOfGraphics
using CSV
using DataFramesMeta
using Dates
PK31 - Turnover II - Intravenous Dosing of Hormone
1 Background
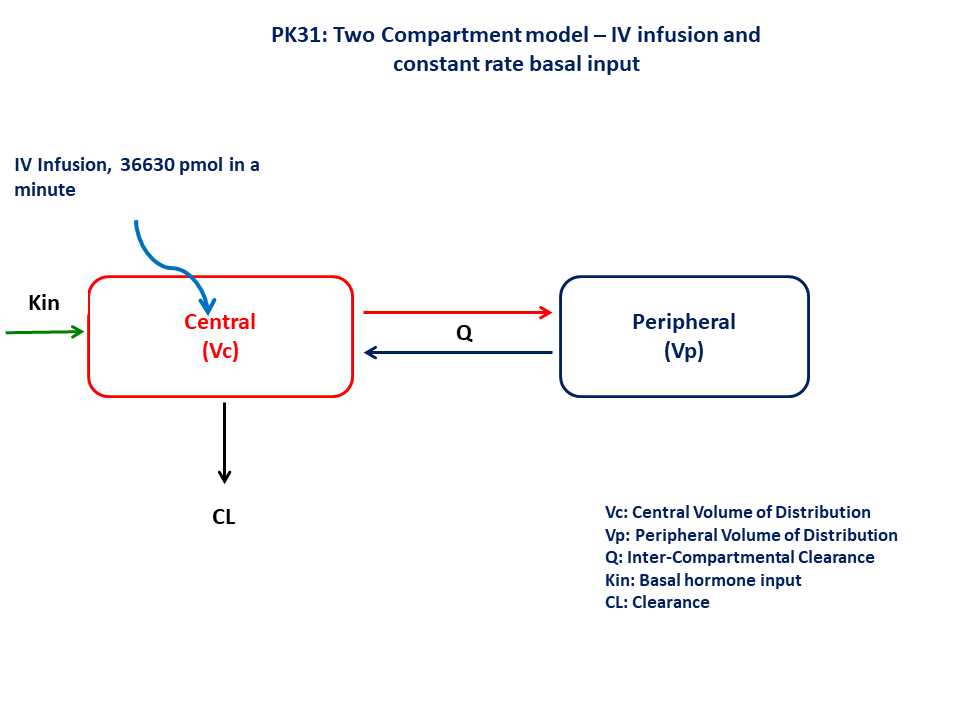
- Structural model - Two compartment with additional input for basal hormone synthesis in the central compartment
- Route of administration - IV infusion (1 minute)
- Dosage Regimen - 36,630 pmol
- Number of Subjects - 1
2 Learning Outcome
In this model, you will learn how to build a two compartment model with additional input for basal hormone level. This model will help to simulate the plasma concentration profile after IV administration, considering basal hormone input.
3 Objectives
- To analyze the intravenous datasets with parallel turnover
- To write a multi-compartment model in terms of differential equations
4 Libraries
Call the necessary libraries to get start.
5 Model
In this one compartment model, we administer an IV infusion dose to the central compartment.
pk_31 = @model begin
@metadata begin
desc = "Two Compartment Model"
timeu = u"hr"
end
@param begin
"""
Basal hormonal input (pmol/hr)
"""
tvkin ∈ RealDomain(lower = 0)
"""
Central Volume of Distribution (L)
"""
tvvc ∈ RealDomain(lower = 0)
"""
Clearance (L/hr)
"""
tvcl ∈ RealDomain(lower = 0)
"""
Intercompartmental Clearance (L/hr)
"""
tvq ∈ RealDomain(lower = 0)
"""
Peripheral Volume of Distribution (L)
"""
tvvp ∈ RealDomain(lower = 0)
Ω ∈ PDiagDomain(5)
"""
Proportional RUV
"""
σ²_prop ∈ RealDomain(lower = 0)
end
@random begin
η ~ MvNormal(Ω)
end
@pre begin
Kin = tvkin * exp(η[1])
Vc = tvvc * exp(η[2])
Cl = tvcl * exp(η[3])
Q = tvq * exp(η[4])
Vp = tvvp * exp(η[5])
end
@dynamics begin
Central' = Kin - (Cl / Vc) * Central - (Q / Vc) * Central + (Q / Vp) * Peripheral
Peripheral' = (Q / Vc) * Central - (Q / Vp) * Peripheral
end
@derived begin
cp = @. Central / Vc
"""
Observed Concentration (pmol/L)
"""
dv ~ @. Normal(cp, sqrt(cp^2 * σ²_prop))
end
endPumasModel
Parameters: tvkin, tvvc, tvcl, tvq, tvvp, Ω, σ²_prop
Random effects: η
Covariates:
Dynamical system variables: Central, Peripheral
Dynamical system type: Matrix exponential
Derived: cp, dv
Observed: cp, dv6 Parameters
The parameters are as given below. Note that tv represents the typical value for parameters.
Kin- Basal hormonal input (pmol/hr)Vc- Central Volume of Distribution (L)Cl- Clearance (L/hr)Q- Intercompartmental Clearance (L/hr)Vp- Peripheral Volume of Distribution (L)Ω- Between Subject Variability,σ- Residual error
param = (
tvkin = 1531.87,
tvvc = 8.8455,
tvcl = 76.5987,
tvq = 56.8775,
tvvp = 58.8033,
Ω = Diagonal([0.04, 0.04, 0.04, 0.04, 0.04]),
σ²_prop = 0.015,
)7 Dosage Regimen
A single dose of 36630 pmol is given as an IV Infusion
ev1 = DosageRegimen(36630, time = 0, cmt = 1, duration = 0.0166)1×10 DataFrame
| Row | time | cmt | amt | evid | ii | addl | rate | duration | ss | route |
|---|---|---|---|---|---|---|---|---|---|---|
| Float64 | Int64 | Float64 | Int8 | Float64 | Int64 | Float64 | Float64 | Int8 | NCA.Route | |
| 1 | 0.0 | 1 | 36630.0 | 1 | 0.0 | 0 | 2.20663e6 | 0.0166 | 0 | NullRoute |
sub1 = Subject(id = 1, events = ev1, observations = (cp = nothing,))Subject
ID: 1
Events: 2
Observations: cp: (n=0)8 Simulation
Simulate the plasma concentration profile
Random.seed!(123)The random effects are zero’ed out since we are simulating a single subject
zfx = zero_randeffs(pk_31, sub1, param)(η = [0.0, 0.0, 0.0, 0.0, 0.0],)sim_sub1 = simobs(pk_31, sub1, param, zfx, obstimes = 0.01:0.0001:32)SimulatedObservations
Simulated variables: cp, dv
Time: 0.01:0.0001:32.09 Visualization
@chain DataFrame(sim_sub1) begin
dropmissing(:cp)
data(_) *
mapping(:time => "Time (hours)", :cp => "Concentration (pmol/L)") *
visual(Lines; linewidth = 4)
draw(;
figure = (; fontsize = 22),
axis = (;
yscale = log10,
ytickformat = i -> (@. string(round(i; digits = 1))),
xticks = 0:5:35,
),
)
end10 Population simulation
par = (
tvkin = 1531.87,
tvvc = 8.8455,
tvcl = 76.5987,
tvq = 56.8775,
tvvp = 58.8033,
Ω = Diagonal([0.09, 0.0125, 0.0225, 0.04, 0.0365]),
σ²_prop = 0.0612144,
)
ev1 = DosageRegimen(36630, time = 0, cmt = 1, duration = 0.0166)
pop = map(i -> Subject(id = i, events = ev1), 1:85)
sim_pop = simobs(
pk_31,
pop,
par,
obstimes = [
0.0167,
0.1167,
0.167,
0.25,
0.583,
0.833,
1.083,
1.583,
2.083,
4.083,
8.083,
12,
23.5,
24.25,
26.75,
32,
],
)
df_sim = DataFrame(sim_pop)
#CSV.write("pk_31.csv", df_sim)