using Pumas
using PumasUtilities
using Random
using CairoMakie
using AlgebraOfGraphics
using CSV
using DataFramesMeta
PK34 - Reversible metabolism
1 Learning Outcome
In this tutorial, you will learn how to simulate
- kinetics of a drug that exhibits reversible metabolism, and
- data for two IV-Infusion regimens with different rates of infusions.
2 Objectives
In this exercise, you will learn how to simulate an IV-infusion two compartment model and the kinetics of reversible metabolism.
3 Background
Before constructing a model, it is important to establish the process the model will follow and a scenario for the simulation.
Below is the scenario for this tutorial:
- Structural model - Two compartment model
- Route of administration - IV-infusion (with an infusion pump)
- Dosage Regimen - 100 mg/m² of Cisplatin for 1 hour at time=0 considering a patient with 1.7 m²
- Number of Subjects - 1
This diagram describes how such an administered dose will be handled, which facilitates building the model. 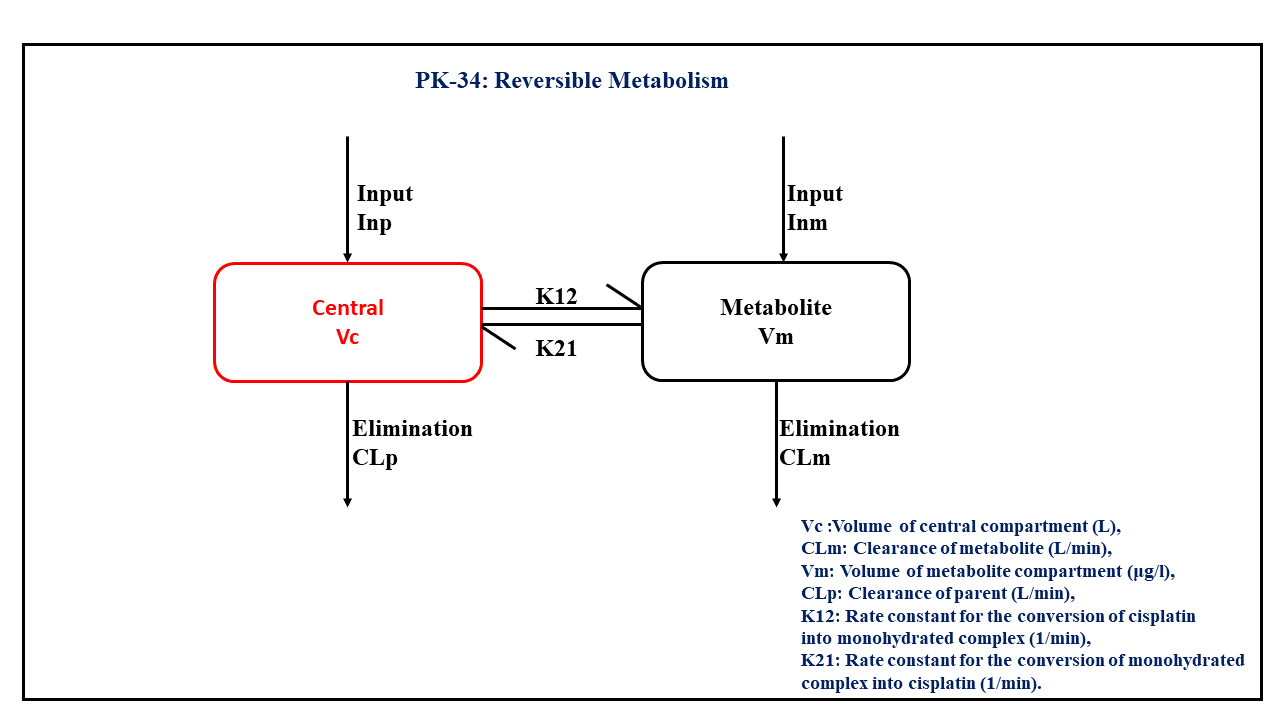
4 Assumptions to Consider
- A fraction of the dose (2.3%) is present as the monohydrated complex in the infusion solution.
- There is a reversible reaction between cisplatin (p) and its monohydrated complex (m).
- The input rate can be split into a cisplatin infusion rate (Inp) and a monohydrate infusion rate (Inm).
5 Libraries
Call the required libraries to get started.
6 Model - Microconstant Model
In this two compartment model, we administer the mentioned dose in the Central compartment and the Metabolite compartment at time = 0. K12 and K21 are rate constants for the conversion of cisplatin into monohydrated complex and the monohydrated complex into cisplatin, respectively.
pk_34 = @model begin
@metadata begin
desc = "Microconstant Model"
timeu = u"minute"
end
@param begin
"""
Volume of Central Compartment (L)
"""
tvvc ∈ RealDomain(lower = 0)
"""
Clearance of metabolite (L/min)
"""
tvclm ∈ RealDomain(lower = 0)
"""
Volume of Metabolite Compartment (μg/L)
"""
tvvm ∈ RealDomain(lower = 0)
"""
Clearance of parent (L/min)
"""
tvclp ∈ RealDomain(lower = 0)
tvk12 ∈ RealDomain(lower = 0)
tvk21 ∈ RealDomain(lower = 0)
Ω ∈ PDiagDomain(6)
"""
Proportional RUV
"""
σ²_prop ∈ RealDomain(lower = 0)
end
@random begin
η ~ MvNormal(Ω)
end
@pre begin
Vc = tvvc * exp(η[1])
CLm = tvclm * exp(η[2])
Vm = tvvm * exp(η[3])
CLp = tvclp * exp(η[4])
K12 = tvk12 * exp(η[5])
K21 = tvk21 * exp(η[6])
end
@dynamics begin
Central' = -(CLp / Vc) * Central - K12 * Central + K21 * Metabolite * Vc / Vm
Metabolite' =
-(CLm / Vm) * Metabolite - K21 * Metabolite + K12 * Central * Vm / Vc
end
@derived begin
cp = @. Central / Vc
"""
Observed Concentration - Cisplatin (μg/ml)
"""
dv_cp ~ @. Normal(cp, sqrt(cp^2 * σ²_prop))
met = @. Metabolite / Vm
"""
Observed Concentration - Metabolite (μg/ml)
"""
dv_met ~ @. Normal(met, sqrt(cp^2 * σ²_prop))
end
endPumasModel
Parameters: tvvc, tvclm, tvvm, tvclp, tvk12, tvk21, Ω, σ²_prop
Random effects: η
Covariates:
Dynamical system variables: Central, Metabolite
Dynamical system type: Matrix exponential
Derived: cp, dv_cp, met, dv_met
Observed: cp, dv_cp, met, dv_met7 Parameters
Parameters provided for simulation are as below.
Vc- Volume of central compartment (L)CLm- Clearance of metabolite (L/min)Vm- Volume of metabolite compartment (μg/L)CLp- Clearance of parent (L/min)K12- Rate constant for the conversion of cisplatin into monohydrated complex (min⁻¹)K21- Rate constant for the conversion of monohydrated complex into cisplatin (min⁻¹)Ω- Between Subject Variabilityσ- Residual error
These are the initial estimates we will be using in this model exercise. Note that tv represents the typical value for parameters.
param = (;
tvvc = 14.1175,
tvclm = 0.00832616,
tvvm = 2.96699,
tvclp = 0.445716,
tvk12 = 0.00021865,
tvk21 = 0.021313,
Ω = Diagonal([0.01, 0.01, 0.01, 0.01, 0.01, 0.01]),
σ²_prop = 0.001,
)8 Dosage Regimen
To start the simulation process, the dosing regimen specified in the background section must be developed first prior to running a simulation.
The dosage regimen is specified as:
- Cisplatin Infusion - A total dose of 170 mg (100 mg/m² * 1.7 m²) split as Cisplatin 166.09 and Monohydrate 3.91.
- Monohydrate Infusion - A total dose of 10 mg/L is given as Monohydrate
This is how to establish the dosing regimen:
ev1 = DosageRegimen([166.09, 3.91]; time = 0, cmt = [1, 2], duration = [60, 60])| Row | time | cmt | amt | evid | ii | addl | rate | duration | ss | route |
|---|---|---|---|---|---|---|---|---|---|---|
| Float64 | Int64 | Float64 | Int8 | Float64 | Int64 | Float64 | Float64 | Int8 | NCA.Route | |
| 1 | 0.0 | 1 | 166.09 | 1 | 0.0 | 0 | 2.76817 | 60.0 | 0 | NullRoute |
| 2 | 0.0 | 2 | 3.91 | 1 | 0.0 | 0 | 0.0651667 | 60.0 | 0 | NullRoute |
This is how to create the single subject undergoing the dosing regimen above.
sub1 = Subject(id = "Cisplatin (Inf-Cisplatin)", events = ev1, time = 20:0.1:180)Subject
ID: Cisplatin (Inf-Cisplatin)
Events: 4The above two steps will be repeated to create the Monohydrate infusion group.
ev2 = DosageRegimen(10; time = 0, cmt = 2, duration = 2)| Row | time | cmt | amt | evid | ii | addl | rate | duration | ss | route |
|---|---|---|---|---|---|---|---|---|---|---|
| Float64 | Int64 | Float64 | Int8 | Float64 | Int64 | Float64 | Float64 | Int8 | NCA.Route | |
| 1 | 0.0 | 2 | 10.0 | 1 | 0.0 | 0 | 5.0 | 2.0 | 0 | NullRoute |
sub2 = Subject(id = "Monohydrate (Inf-Cisplatin)", events = ev2, time = 5:0.1:180)Subject
ID: Monohydrate (Inf-Cisplatin)
Events: 2Creating the population:
pop2_sub = [sub1, sub2]Population
Subjects: 2
Observations: 9 Simulation
We will simulate the plasma concentration at the pre-specified time points.
Random.seed!()
The Random.seed! function is included here for purposes of reproducibility of the simulation in this tutorial. Specification of a seed value would not be required in a Pumas workflow that is estimating model parameters.
Random.seed!(123)sim_sub1 = simobs(pk_34, pop2_sub, param)Simulated population (Vector{<:Subject})
Simulated subjects: 2
Simulated variables: cp, dv_cp, met, dv_met10 Visualization
From the plots, we can see the plasma and metabolite concentrations for both infusion groups.
We will first convert the simulation results into a DataFrame to facilitate plotting.
df_plot = DataFrame(sim_sub1)This plot is for the parent drug:
@chain df_plot begin
dropmissing(:cp)
data(_) *
mapping(
:time => "Time (hours)",
:cp => "Parent concentration (μg/mL)";
color = :id => "Infusion group",
) *
visual(Lines; linewidth = 4)
draw(;
figure = (; fontsize = 22),
axis = (; xticks = 0:20:180),
legend = (; position = :bottom),
)
endThis plot is for the metabolite:
@chain df_plot begin
dropmissing(:met)
data(_) *
mapping(
:time => "Time (hours)",
:met => "Metabolite concentration (μg/mL)";
color = :id => "Infusion group",
) *
visual(Lines; linewidth = 4)
draw(;
figure = (; fontsize = 22),
axis = (; xticks = 0:20:180),
legend = (; position = :bottom),
)
end11 Conclusion
In this tutorial, a drug with two IV-Infusion regimens, which exhibits reversible metabolism, was fit to a model. Constructing a model such as this involves:
- understanding the process of how the drug and metabolite are passed through the system,
- quantitatively explaining non-linear kinetics of elimination, and
- simulating the model in a single patient for evaluation.