using Random
using Pumas
using PumasUtilities
using AlgebraOfGraphics
using CairoMakie
using CSV
using DataFramesMeta
using Dates
PK46 - Long Infusion and Short Half-Life
1 Background
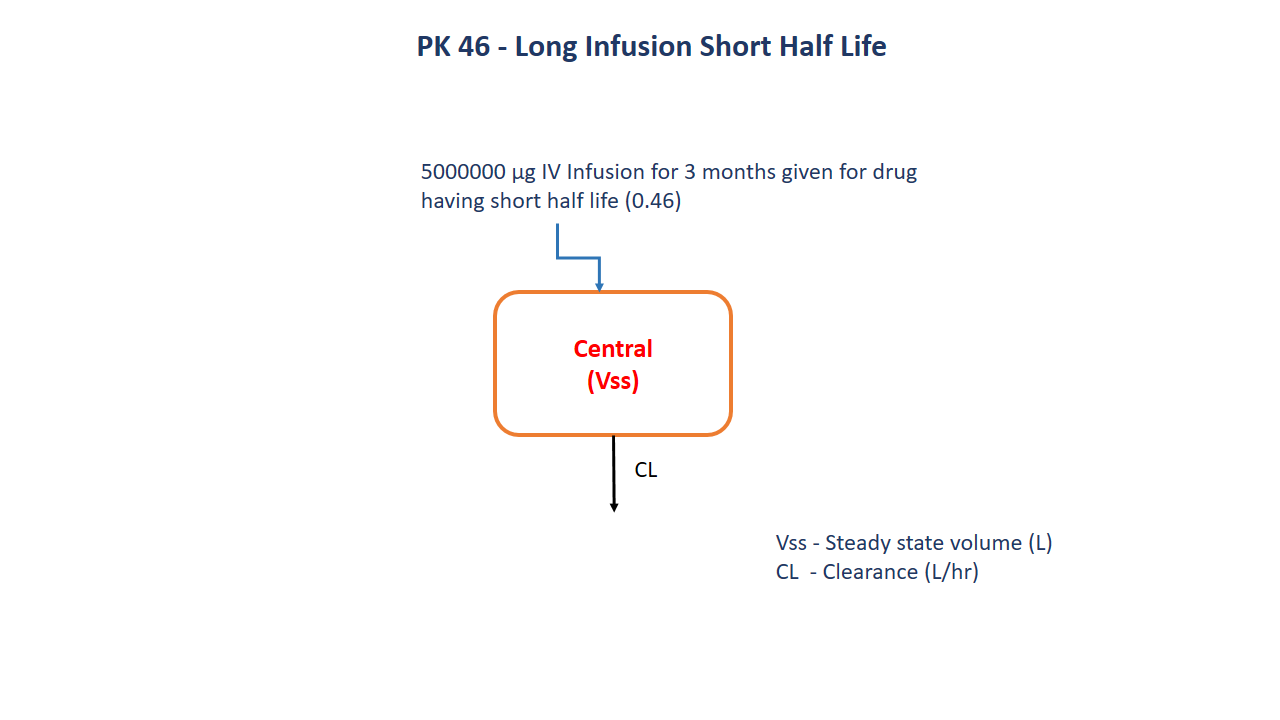
- Structural model - Long infusion short half life one compartment model
- Route of administration - IV infusion
- Dosage Regimen - 500000 μg
- Number of Subjects - 1
2 Learning Outcome
This exercise deals with the drug having a short half life.
3 Objectives
To build a model for a drug having a short half life given as a very long infusion of up to 3 months.
4 Libraries
Call the necessary libraries to get started.
5 Model
To build a one compartment model for a drug having a short half life given a long infusion for 3 months.
pk_46 = @model begin
@metadata begin
desc = "One Compartment Model"
timeu = u"hr"
end
@param begin
"""
Volume at Steady State (L)
"""
tvvss ∈ RealDomain(lower = 0)
"""
Clearance (L/hr)
"""
tvcl ∈ RealDomain(lower = 0)
Ω ∈ PDiagDomain(2)
"""
Additive Error
"""
σ_add ∈ RealDomain(lower = 0)
end
@random begin
η ~ MvNormal(Ω)
end
@pre begin
Vss = tvvss * exp(η[1])
Cl = tvcl * exp(η[2])
end
@dynamics begin
Central' = -(Cl / Vss) * Central
end
@derived begin
cp = @. Central / Vss
"""
Observed Concentration (μg/L)
"""
dv ~ @. Normal(cp, σ_add)
end
endPumasModel
Parameters: tvvss, tvcl, Ω, σ_add
Random effects: η
Covariates:
Dynamical system variables: Central
Dynamical system type: Matrix exponential
Derived: cp, dv
Observed: cp, dv6 Parameters
Parameters provided for simulation are as below. Note that tv represents the typical value for parameters.
Vss- Steady state volume (L)CL- Clearance (L/hr)
param = (; tvvss = 35.6, tvcl = 61, Ω = Diagonal([0.04, 0.04]), σ_add = 0.196337)7 Dosage Regimen
A dose of 500000 μg was given as an Intravenous Infusion to a single subject for over 3 months.
ev1 = DosageRegimen(500000, time = 0, cmt = 1, duration = 2016)1×10 DataFrame
| Row | time | cmt | amt | evid | ii | addl | rate | duration | ss | route |
|---|---|---|---|---|---|---|---|---|---|---|
| Float64 | Int64 | Float64 | Int8 | Float64 | Int64 | Float64 | Float64 | Int8 | NCA.Route | |
| 1 | 0.0 | 1 | 500000.0 | 1 | 0.0 | 0 | 248.016 | 2016.0 | 0 | NullRoute |
sub1 = Subject(id = 1, events = ev1)Subject
ID: 1
Events: 28 Simulation
Simulate the data after the administration of an infusion
Random.seed!(123)The random effects are zero’ed out since we are simulating a single subject
zfx = zero_randeffs(pk_46, sub1, param)(η = [0.0, 0.0],)sim_sub1 = simobs(pk_46, sub1, param, zfx, obstimes = 0.5:0.1:2100)SimulatedObservations
Simulated variables: cp, dv
Time: 0.5:0.1:2100.09 Visualization
@chain DataFrame(sim_sub1) begin
dropmissing(:cp)
data(_) *
mapping(:time => "Time (hours)", :cp => "Concentration (μg/L)") *
visual(Lines; linewidth = 4)
draw(; figure = (; fontsize = 22), axis = (; xticks = 0:500:2000))
endThe plot below shows the decline in the concentrations after the end of the infusion
@chain DataFrame(sim_sub1) begin
@rsubset 2016 ≤ :time < 2020
data(_) *
mapping(:time => "Time (hours)", :cp => "Concentration (μg/L)") *
visual(ScatterLines; linewidth = 4)
draw(;
axis = (;
yscale = Makie.Symlog10(10.0),
limits = (nothing, (-0.1, nothing)),
xticks = 2015:1:2020,
),
)
end10 Simulating a Population
par = (; tvvss = 35.6, tvcl = 61, Ω = Diagonal([0.0125, 0.0224]), σ_add = 0.196337)
ev1 = DosageRegimen(500000, time = 0, cmt = 1, duration = 2016)
pop = map(i -> Subject(id = i, events = ev1), 1:72)
Random.seed!(1234)
sim_pop =
simobs(pk_46, pop, par, obstimes = [0.5, 24, 96, 168, 672, 2016, 2016.5, 2017, 2018])
df_sim = DataFrame(sim_pop)
#CSV.write("pk_46.csv", df_sim)